题目内容
3.已知一次函数y=kx+b的图象经过点A(3,0),与y轴交于点B,若△AOB的面积为6,试求点B的坐标.解:当x=0时,y=b,
∴直线y=kx+b与y轴的交点B的坐标是(0,b)
∴BO=|b|
∵A(3,0),∴AO=3,∴S△AOB=$\frac{1}{2}$AO•BO=6,
∴$\frac{1}{2}$×3×|b|=6,∴b=4或-4
∴点B的坐标是(0,4)或(0,-4).
分析 将x=0代入一次函数解析式中可求出点B的坐标,进而即可得出OB的长度,由点A的坐标可得出OA的长度,根据三角形的面积公式结合△AOB的面积为6,即可得出关于b的含绝对值符号的一元一次方程,解之即可得出b值,此题得解.
解答 解:当x=0时,y=b,
∴直线y=kx+b与y轴的交点B的坐标是(0,b),
∴BO=|b|.
∵A(3,0),
∴AO=3,
∴S△AOB=$\frac{1}{2}$AO•BO=6,
∴$\frac{1}{2}$×3×|b|=6,
∴b=4或-4,
∴点B的坐标是(0,4)或(0,-4).
故答案为:b;0;b;|b|;|b|;4;-4;(0,4);(0,-4).
点评 本题考查了一次函数图象上点的坐标特征以及三角形的面积,根据三角形的面积公式结合△AOB的面积为6列出关于b的含绝对值符号的一元一次方程是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.某种商品的标价是132元,若以标价的9折销售,仍可获利润10%,则该商品的进价为( )
| A. | 105元 | B. | 108元 | C. | 110元 | D. | 118元 |
18.下列语句正确的个数是( )
①两条直线相交有两个角是直角,那么这两条直线垂直;
②若两条直线互相垂直,则相交所成的四个角都是直角;
③互相垂直的两条直线的交点叫做垂直;
④平面内,两条互相垂直的线段不一定相交,但它们所在的直线一定相交.
①两条直线相交有两个角是直角,那么这两条直线垂直;
②若两条直线互相垂直,则相交所成的四个角都是直角;
③互相垂直的两条直线的交点叫做垂直;
④平面内,两条互相垂直的线段不一定相交,但它们所在的直线一定相交.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.一组按规律排列的式子:a2,$\frac{{a}^{4}}{2}$,$\frac{{a}^{6}}{3}$,$\frac{{a}^{8}}{4}$,…,则第2016个式子是( )
| A. | $\frac{{a}^{2016}}{2015}$ | B. | $\frac{{a}^{2016}}{2016}$ | C. | $\frac{{a}^{4030}}{2015}$ | D. | $\frac{{a}^{4032}}{2016}$ |
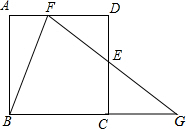 如图,在正方形ABCD中,E是CD的中点,F是AD的一个三等分点,设BC的延长线与FE的延长线相交于G.问BF是否平分∠AFG?请说明理由.
如图,在正方形ABCD中,E是CD的中点,F是AD的一个三等分点,设BC的延长线与FE的延长线相交于G.问BF是否平分∠AFG?请说明理由. 如图,线段AB=10cm,点C为线段AB上任意一点,点M为AC的中点,点N为BC的中点,则MN=5cm.
如图,线段AB=10cm,点C为线段AB上任意一点,点M为AC的中点,点N为BC的中点,则MN=5cm.