题目内容
19．已知二次函数y=ax2+bx+c的图象经过点（-1，-6）、（1，4）和（3，6），求这个二次函数的表达式．分析 把三点坐标代入二次函数解析式求出a，b，c的值，即可确定出二次函数解析式．
解答 解：∵二次函数y=ax2+bx+c的图象经过点（-1，-6）、（1，4）和（3，6），
∴$\left\{\begin{array}{l}{a-b+c=-6}\\{a+b+c=4}\\{9a+3b+c=6}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=-1}\\{b=5}\\{c=0}\end{array}\right.$．
则这个二次函数的表达式为y=-x2+5x．
点评 此题考查了待定系数法求二次函数解析式，熟练掌握待定系数法是解本题的关键．
练习册系列答案
相关题目
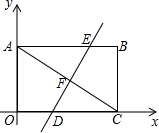如图，平面直角坐标系中，把矩形OABC沿直线DE对折使点C落在点A（0，6）处，DE与AC相交于点F，且$\frac{EF}{AF}$=$\frac{\sqrt{3}}{3}$．
如图，已知在⊙O中M是弧AB的中点，N是弦AB的中点，AB=2$\sqrt{3}$，MN=1，求：圆心到AB的距离．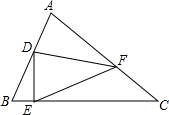
如图，在△ABC中，∠ACB=45°，D是AB边的中点，点E在BC边上，点F在AC边上，DE⊥DF，连接EF，若BE=1，EF=5，则线段AF的长为3$\sqrt{2}$．
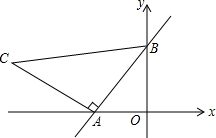如图，在直角坐标系中，直线y=$\frac{4}{3}$x+8与x轴相交于点A，与y轴相交于点B．