题目内容
13.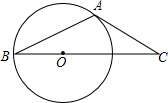 如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )
如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )| A. | 110° | B. | 115° | C. | 120° | D. | 130° |
分析 连结OA,如图,先根据切线的性质得∠OAC=90°,则利用互余可计算出∠AOC=90°-∠C=50°,再根据等腰三角形的性质和三角形外角性质可计算出∠OAB=25°,然后计算∠OAB+∠OAC即可.
解答 解:连结OA,如图,
∵AC为切线,
∴OA⊥AC,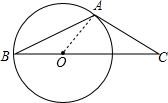
∴∠OAC=90°,
∴∠AOC=90°-∠C=90°-40°=50°,
∵OA=OB,
∴∠B=∠OAB,
而∠AOC=∠B+∠OAB,
∴∠OAB=$\frac{1}{2}$∠AOC=25°,
∴∠BAC=∠OAB+∠OAC=25°+90°=115°.
故选B.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
4.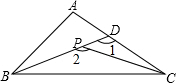 如图,P是△ABC内一点,延长CP交AB于D,则下列不等式成立的是( )
如图,P是△ABC内一点,延长CP交AB于D,则下列不等式成立的是( )
 如图,P是△ABC内一点,延长CP交AB于D,则下列不等式成立的是( )
如图,P是△ABC内一点,延长CP交AB于D,则下列不等式成立的是( )| A. | ∠2>∠A>∠1 | B. | ∠2>∠1>∠A | C. | ∠1>∠A>∠2 | D. | ∠A>∠1>∠2 |
18. 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )
 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
5. 实数x、y、z在数轴上的位置如图所示,则下列关系正确的是( )
实数x、y、z在数轴上的位置如图所示,则下列关系正确的是( )
 实数x、y、z在数轴上的位置如图所示,则下列关系正确的是( )
实数x、y、z在数轴上的位置如图所示,则下列关系正确的是( )| A. | x+y+z>0 | B. | x+y+z<0 | C. | xy<yz | D. | xy<xz |
2.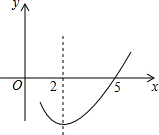 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(5,0),对称轴为直线x=2,则下列结论中正确的是( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(5,0),对称轴为直线x=2,则下列结论中正确的是( )
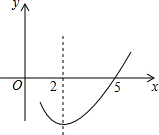 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(5,0),对称轴为直线x=2,则下列结论中正确的是( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(5,0),对称轴为直线x=2,则下列结论中正确的是( )| A. | 当x>2时,y随x增大而减小 | B. | 4a=b | ||
| C. | 图象过点(-1,0) | D. | 9a+3b+c>0 |
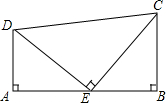 如图,已知CE=DE,∠A=∠B=CED=90°,若AB=5,BC=3,求AD的长.
如图,已知CE=DE,∠A=∠B=CED=90°,若AB=5,BC=3,求AD的长.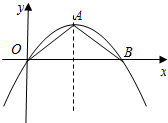 如图,已知抛物线y=-$\frac{1}{4}$x2+x的顶点为A,经过原点O,与x轴的另一个交点为B.在抛物线上求点M,使△AOB的面积是△MOB面积的2倍.
如图,已知抛物线y=-$\frac{1}{4}$x2+x的顶点为A,经过原点O,与x轴的另一个交点为B.在抛物线上求点M,使△AOB的面积是△MOB面积的2倍.