题目内容
18. 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
分析 根据题意可得AH平分∠CAB,再根据平行线的性质可得∠CAB的度数,再根据角平分线的性质可得答案.
解答 解:由题意可得:AH平分∠CAB,
∵AB∥CD,
∴∠C+∠CAB=180°,
∵∠ACD=140°,
∴∠CAB=40°,
∵AH平分∠CAB,
∴∠HAB=20°,
∴∠AHC=20°.
故选A.
点评 此题主要考查了平行线的性质,以及角平分线的作法,关键是掌握两直线平行,同旁内角互补,以及角平分线的做法.

练习册系列答案
相关题目
13.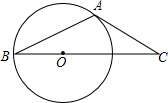 如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )
如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )
 如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )
如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )| A. | 110° | B. | 115° | C. | 120° | D. | 130° |
10.下列说法其中正确的有( )
(1)最小的正整数是1,最大的负整数是-1;
(2)相反数等于它本身的数只有0,倒数等于它本身的数是±1
(3)绝对值等于它本身的数是非负数,绝对值等于它的相反数的数是非正数
(4)绝对值相等的两个数一定相等,绝对值不相等的两个数一定不相等.
(1)最小的正整数是1,最大的负整数是-1;
(2)相反数等于它本身的数只有0,倒数等于它本身的数是±1
(3)绝对值等于它本身的数是非负数,绝对值等于它的相反数的数是非正数
(4)绝对值相等的两个数一定相等,绝对值不相等的两个数一定不相等.
| A. | (1),(2),(3) | B. | (2),(3),(4) | C. | (1),(3),(4) | D. | (1),(2),(3),(4) |
8.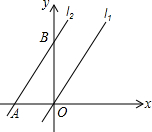 如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,直线l2与x、y轴分别交于点A、B,且l1∥l2,OA=2,则线段OB的长为( )
如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,直线l2与x、y轴分别交于点A、B,且l1∥l2,OA=2,则线段OB的长为( )
 如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,直线l2与x、y轴分别交于点A、B,且l1∥l2,OA=2,则线段OB的长为( )
如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,直线l2与x、y轴分别交于点A、B,且l1∥l2,OA=2,则线段OB的长为( )| A. | 3 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
 如图,用一个平面从正方体的三个顶点处截去正方体的一角变成一个新的多面体,这个多面体共有12条棱.
如图,用一个平面从正方体的三个顶点处截去正方体的一角变成一个新的多面体,这个多面体共有12条棱. 如图是一数值转换机,若输出的结果为-48,则输入的x的值为±4.
如图是一数值转换机,若输出的结果为-48,则输入的x的值为±4.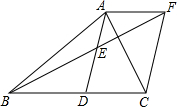 如图,在△ABC中,AD是BC边的中线,E是AD的中点,过A点作AF∥BC交BE的延长线于点F,连结CF.求证:四边形ADCF是平行四边形.
如图,在△ABC中,AD是BC边的中线,E是AD的中点,过A点作AF∥BC交BE的延长线于点F,连结CF.求证:四边形ADCF是平行四边形. 如图,已知圆周角∠ACB的度数为100°,则圆周角∠D的度数等于80°.
如图,已知圆周角∠ACB的度数为100°,则圆周角∠D的度数等于80°.