题目内容
3.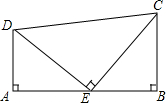 如图,已知CE=DE,∠A=∠B=CED=90°,若AB=5,BC=3,求AD的长.
如图,已知CE=DE,∠A=∠B=CED=90°,若AB=5,BC=3,求AD的长.
分析 根据余角的性质得到∠ADE=∠BEC,推出△ADE≌△BCE,根据全等三角形的性质得到AD=BE,AE=BC=2,即可得到结论.
解答 解:∵∠A=∠B=∠CED=90°,
∴∠ADE+∠AED=∠AED+∠BEC=90°,
∴∠ADE=∠BEC,
在△ADE与△BEC中,$\left\{\begin{array}{l}{∠ADE=∠BEC}\\{∠A=∠B}\\{DE=CE}\end{array}\right.$,
∴△ADE≌△BCE,
∴AD=BE,AE=BC=2,
∵AB=5,
∴AD=BE=2.
点评 本题考查了全等三角形的判定和性质,余角的性质,熟练正确全等三角形的判定和性质是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
13.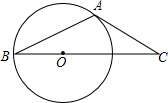 如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )
如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )
 如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )
如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )| A. | 110° | B. | 115° | C. | 120° | D. | 130° |
 如图,AB,CD相交于点O,点E,F在AB上,AE=BF,AD=BC,AD∥BC.求证:OE=OF.
如图,AB,CD相交于点O,点E,F在AB上,AE=BF,AD=BC,AD∥BC.求证:OE=OF.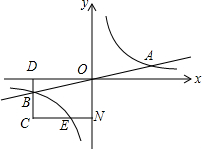 已知双曲线y=$\frac{k}{x}$与直线y=$\frac{1}{4}$x相交于A、B两点.过点B作矩形DCNO交x轴于点D.交Y轴于点N.交双曲线y=$\frac{k}{x}$于点E.若B是CD的中点,四边形OBCE的面积为4,则双曲线y=$\frac{k}{x}$的解析式为$\frac{4}{x}$.
已知双曲线y=$\frac{k}{x}$与直线y=$\frac{1}{4}$x相交于A、B两点.过点B作矩形DCNO交x轴于点D.交Y轴于点N.交双曲线y=$\frac{k}{x}$于点E.若B是CD的中点,四边形OBCE的面积为4,则双曲线y=$\frac{k}{x}$的解析式为$\frac{4}{x}$. 如图,用一个平面从正方体的三个顶点处截去正方体的一角变成一个新的多面体,这个多面体共有12条棱.
如图,用一个平面从正方体的三个顶点处截去正方体的一角变成一个新的多面体,这个多面体共有12条棱.