题目内容
1.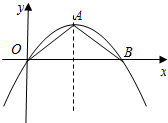 如图,已知抛物线y=-$\frac{1}{4}$x2+x的顶点为A,经过原点O,与x轴的另一个交点为B.在抛物线上求点M,使△AOB的面积是△MOB面积的2倍.
如图,已知抛物线y=-$\frac{1}{4}$x2+x的顶点为A,经过原点O,与x轴的另一个交点为B.在抛物线上求点M,使△AOB的面积是△MOB面积的2倍.
分析 设M(t,-$\frac{1}{4}$t2+t),通过解方程-$\frac{1}{4}$x2+x=0可得到B(4,0),再把解析式配成顶点式得到A(2,1),则根据三角形面积公式得到S△AOB=2,由于△AOB的面积是△MOB面积的2倍,所以$\frac{1}{2}$×4×|-$\frac{1}{4}$t2+t|=$\frac{1}{2}$×2,然后解方程-$\frac{1}{4}$t2+t=$\frac{1}{2}$和方程-$\frac{1}{4}$t2+t=-$\frac{1}{2}$求出t的值即可得到M点坐标.
解答 解:设M(t,-$\frac{1}{4}$t2+t),
当y=0时,-$\frac{1}{4}$x2+x=0,解得x1=0,x2=4,则B(4,0),
而y=-$\frac{1}{4}$x2+x=-$\frac{1}{4}$(x-2)2+1,则A(2,1),
所以S△AOB=$\frac{1}{2}$×4×1=2,
因为△AOB的面积是△MOB面积的2倍,
所以$\frac{1}{2}$×4×|-$\frac{1}{4}$t2+t|=$\frac{1}{2}$×2,
则-$\frac{1}{4}$t2+t=$\frac{1}{2}$或-$\frac{1}{4}$t2+t=-$\frac{1}{2}$,
解方程-$\frac{1}{4}$t2+t=$\frac{1}{2}$得t1=2+$\sqrt{2}$,t2=2-$\sqrt{2}$,此时M点坐标为(2+$\sqrt{2}$,$\frac{1}{2}$)或(2-$\sqrt{2}$,$\frac{1}{2}$);
解方程-$\frac{1}{4}$t2+t=-$\frac{1}{2}$得t1=2+$\sqrt{6}$,t2=2-$\sqrt{6}$,此时M点坐标为(2+$\sqrt{6}$,-$\frac{1}{2}$)或(2-,-$\frac{1}{2}$);
所以满足条件的M点的坐标为(2+$\sqrt{2}$,$\frac{1}{2}$)或(2-$\sqrt{2}$,$\frac{1}{2}$)或(2+$\sqrt{6}$,-$\frac{1}{2}$)或(2-,-$\frac{1}{2}$).
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.

 天天练口算系列答案
天天练口算系列答案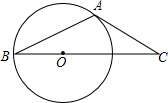 如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )
如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )| A. | 110° | B. | 115° | C. | 120° | D. | 130° |
(1)最小的正整数是1,最大的负整数是-1;
(2)相反数等于它本身的数只有0,倒数等于它本身的数是±1
(3)绝对值等于它本身的数是非负数,绝对值等于它的相反数的数是非正数
(4)绝对值相等的两个数一定相等,绝对值不相等的两个数一定不相等.
| A. | (1),(2),(3) | B. | (2),(3),(4) | C. | (1),(3),(4) | D. | (1),(2),(3),(4) |
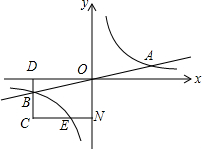 已知双曲线y=$\frac{k}{x}$与直线y=$\frac{1}{4}$x相交于A、B两点.过点B作矩形DCNO交x轴于点D.交Y轴于点N.交双曲线y=$\frac{k}{x}$于点E.若B是CD的中点,四边形OBCE的面积为4,则双曲线y=$\frac{k}{x}$的解析式为$\frac{4}{x}$.
已知双曲线y=$\frac{k}{x}$与直线y=$\frac{1}{4}$x相交于A、B两点.过点B作矩形DCNO交x轴于点D.交Y轴于点N.交双曲线y=$\frac{k}{x}$于点E.若B是CD的中点,四边形OBCE的面积为4,则双曲线y=$\frac{k}{x}$的解析式为$\frac{4}{x}$. 如图是一数值转换机,若输出的结果为-48,则输入的x的值为±4.
如图是一数值转换机,若输出的结果为-48,则输入的x的值为±4.