题目内容
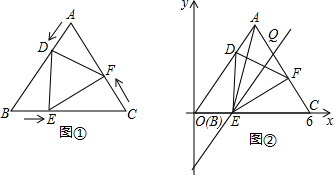
14.平面直角坐标系xOy中,A点的坐标为(0,5).B、C分别是x轴、y轴上的两个动点,C从A出发,沿y轴负半轴方向以1个单位/秒的速度向点O运动,点B从O出发,沿x轴正半轴方向以1个单位/秒的速度运动.设运动时间为t秒,点D是线段OB上一点,且BD=OC.点E是第一象限内一点,且AE${\;}_{=}^{∥}$DB.(1)当t=4秒时,求过E、D、B三点的抛物线解析式.
(2)当0<t<5时,(如图甲),∠ECB的大小是否随着C、B的变化而变化?如果不变,求出它的大小.
(3)求证:∠APC=45°.
(4)当t>5时,(如图乙)∠APC的大小还是45°吗?请说明理由.
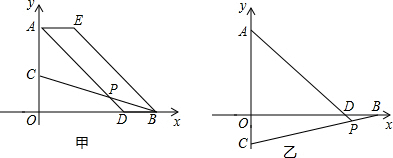
分析 (1)首先根据题意得到E(1,5),B(4,0),D(3,0),然后设过E、D、B三点的抛物线的解析式为y=ax2+bx+c(a≠0),待定系数法求出a、b和c的值;
(2)连接CE,根据SAS证明Rt△ACE≌Rt△OBC,即可CE=CB,∠ACE=∠OBC,∠AEC=∠OCB,结合角角之间的关系即可证明∠ECB=90°;
(3)由(2)知,CE=CB,∠ECB=90°,四边形ADBE是平行四边形,于是得到∠APC=∠EBC;
(4)在第二象限取点F,作AF$\underset{∥}{=}$BD,连接CF、BF,根据SAS证明Rt△ACF≌Rt△OBC,结合外角的性质即可证明∠APC>45°.
解答 解:(1)当t=4秒时,AC=OB=4,由A(0,5)得C(0,1),即OC=1,又BD=OC,AE∥DB且AE=BD,
∴AE=DB=OC=1,
∴E(1,5),B(4,0),D(3,0),
设过E、D、B三点的抛物线的解析式为y=ax2+bx+c(a≠0),
则有$\left\{\begin{array}{l}5=a+b+c\\ o=16a+4b+c\\ o=9a+3b+c\end{array}\right.$解得$\left\{\begin{array}{l}a=+\frac{5}{6}\\ b=-\frac{35}{6}\\ c=10\end{array}\right.$,
∴抛物线解析式为$y=\frac{5}{6}{x^2}-\frac{35}{6}x+10$.
(2)∠ECB的大小不变,
如图1,连接CE,易得Rt△ACE≌Rt△OBC(SAS),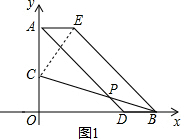
∴CE=CB,∠ACE=∠OBC,∠AEC=∠OCB,
又知∠ACE+∠AEC=90°,
∴∠ACE+∠OCB=90°,
∴∠ECB=90°;
(3)由(2)知,CE=CB,∠ECB=90°,
∴△ECB是等腰直角三角形,
∴∠EBC=45°,
∵AE∥DB且AE=BD,
∴四边形ADBE是平行四边形,
∴AB∥BE,
∴∠APC=∠EBC=45°;
(4)当t>5时,∠APC>45°,
理由如下:
如图2,在第二象限取点F,作AF$\underset{∥}{=}$BD,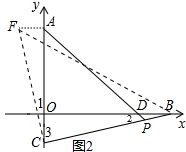
连接CF、BF,易得Rt△ACF≌Rt△OBC(SAS),
∴CF=CB,∠1=∠2,
又∵∠1+∠3=90°,
∴∠2+∠3=90°,
∴△BCF是等腰直角三角形,
∴∠CBF=45°,
∵∠APC>∠CBF(外角大于它不相邻的内角),
∴∠APC>45°.
点评 本题主要考查了二次函数综合题的知识,此题涉及到了待定系数法求二次函数解析式,平行四边形的判定与性质,等腰直角三角形的判定、全等三角形的判定与性质以及三角形外角的性质,解答本题的关键是熟练利用SAS证明直角三角形的全等以及合理地作出辅助线,此题有一定的难度.

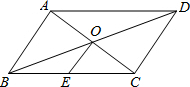 如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )| A. | 3cm | B. | 6cm | C. | 9cm | D. | 12cm |
| A. |  | B. |  | C. |  | D. |  |
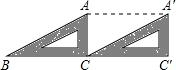 如图,将三角尺ABC沿BC方向平移,得到三角形A′CC′.已知∠B=30°,∠ACB=90°,则∠BAA′的度数为150°.
如图,将三角尺ABC沿BC方向平移,得到三角形A′CC′.已知∠B=30°,∠ACB=90°,则∠BAA′的度数为150°.