题目内容
15. 如图,等腰△ABC的腰长AB=AC=8cm,∠ABC,∠ACB的平分线交于点O,过O作MN∥BC,则△AMN的周长为16cm.
如图,等腰△ABC的腰长AB=AC=8cm,∠ABC,∠ACB的平分线交于点O,过O作MN∥BC,则△AMN的周长为16cm.
分析 根据角平分线的定义可得∠ABO=∠OBC,再根据两直线平行,内错角相等可得∠OBC=∠BOM,从而得到∠ABO=∠BOM,根据等角对等边的性质可得BM=OM,同理可得CN=ON,然后求出△AMN的周长=AB+AC,代入数据进行计算即可.
解答 解:∵OB平分∠ABC,
∴∠ABO=∠OBC,
∵MN∥BC,
∴∠OBC=∠BOM,
∴∠ABO=∠BOM,
∴BM=OM,
同理可得CN=ON,
∴△AMN的周长=AM+MO+ON+AN=AM+BM+CN+AN=AB+AC,
∵AB=8cm,AC=8cm,
∴△AMN的周长=8+8=16cm.
故答案为:16cm.
点评 本题考查了等腰三角形的判定与性质,用到的知识点是等角对等边,两直线平行,内错角相等,熟记性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
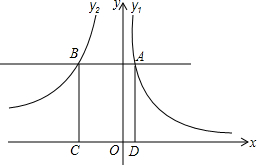 如图,反比例函数y1=$\frac{2}{x}$(x>0)与y2=$\frac{-6}{x}$(x<0),点A是y1上一动点,过点A作x轴的平行线交y轴于点B,过点A、B作x轴的垂线,垂足为D、C.
如图,反比例函数y1=$\frac{2}{x}$(x>0)与y2=$\frac{-6}{x}$(x<0),点A是y1上一动点,过点A作x轴的平行线交y轴于点B,过点A、B作x轴的垂线,垂足为D、C.