Question

5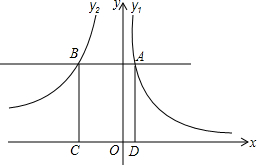．如图，反比例函数y₁=$\frac{2}{x}$（x＞0）与y₂=$\frac{-6}{x}$（x＜0），点A是y₁上一动点，过点A作x轴的平行线交y轴于点B，过点A、B作x轴的垂线，垂足为D、C．
（1）当四边形ABCD为正方形时，求点A的坐标；
（2）当四边形ABCD的周长为12时，求点A的坐标．

Answer 1

分析 （1）根据反比例函数图象上点的坐标特征，设A（a，$\frac{2}{a}$）（a＞0），再确定B（-3a，$\frac{2}{a}$），则AB=4a，AD=$\frac{2}{a}$，则根据正方形的边长相等得到4a=$\frac{2}{a}$，解得a=$\frac{\sqrt{2}}{2}$或a=-$\frac{\sqrt{2}}{2}$（舍去），然后写出点A的坐标；
（2）设A（a，$\frac{2}{a}$）（a＞0），与（1）一样可得B（-3a，$\frac{2}{a}$），AB=4a，AD=$\frac{2}{a}$，利用矩形周长定义得到2（4a+$\frac{2}{a}$）=12，整理得2a²-3a+1=0，解方程求出a即可得到A点坐标．

解答 解：（1）设A（a，$\frac{2}{a}$）（a＞0），
∵AB∥x轴，
∴B点的纵坐标为$\frac{2}{a}$，
而点B在函数y₂=$\frac{-6}{x}$（x＜0）的图象上，
∴B（-3a，$\frac{2}{a}$），
∴AB=a-（-3a）=4a，
而AD=$\frac{2}{a}$，
∵四边形ABCD为正方形，
∴4a=$\frac{2}{a}$，解得a=$\frac{\sqrt{2}}{2}$或a=-$\frac{\sqrt{2}}{2}$（舍去），
∴点A的坐标为（$\frac{\sqrt{2}}{2}$，2$\sqrt{2}$）；
（2）设A（a，$\frac{2}{a}$）（a＞0），与（1）一样可得B（-3a，$\frac{2}{a}$），
AB=a-（-3a）=4a，而AD=$\frac{2}{a}$，
根据题意得2（4a+$\frac{2}{a}$）=12，
整理得2a²-3a+1=0，解得a₁=$\frac{1}{2}$，a₂=1，
所以A点坐标为（$\frac{1}{2}$，4）或（1，2）．

点评 本题考查了反比例函数图象上点的坐标特征：反比例函数y=$\frac{k}{x}$（k为常数，k≠0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即xy=k．