题目内容
9.(1)计算:2cos45°-|-$\sqrt{2}$|+3-1(2)化简 $\frac{{a}^{2}-1}{a}$÷(a-$\frac{2a-1}{a}$)
分析 (1)原式第一项利用特殊角的三角函数值计算,第二项利用绝对值的代数意义化简,最后一项利用负整数指数幂法则计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=2×$\frac{\sqrt{2}}{2}$-$\sqrt{2}$+$\frac{1}{9}$=$\frac{1}{9}$;
(2)原式=$\frac{{a}^{2}-1}{a}$÷$\frac{{a}^{2}-2a+1}{a}$=$\frac{{a}^{2}-1}{a}$•$\frac{a}{(a-1)^{2}}$=$\frac{a+1}{a-1}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.一次函数y=kx+k,且y随x的增大而减小,那么反比例函数y=$\frac{k}{x}$满足( )
| A. | 当x>0时,y>0 | B. | 在每个象限内,y随x的增大而减小 | ||
| C. | 图象分布在第一、三象限 | D. | 图象分布在第二、四象限 |
17.已知两直线y1=kx+k-1、y2=(k+1)x+k(k为正整数),设这两条直线与x轴所围成的三角形的面积为Sk,则S1+S2+S3+…+S2013的值是$\frac{2013}{4028}$.
18.(2+1)(22+1)(24+1)(28+1)…(232+1)+1 的个位数字为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
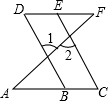 如图,已知B、E分别是AC、DF上的点,∠1=∠2,∠C=∠D.∠ABD与∠C相等吗?为什么?
如图,已知B、E分别是AC、DF上的点,∠1=∠2,∠C=∠D.∠ABD与∠C相等吗?为什么?