题目内容
18.(2+1)(22+1)(24+1)(28+1)…(232+1)+1 的个位数字为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 先把(2+1)变成22-1,然后逐个使用平方差公式,算出结果,再根据2的任何次幂的个位数字的规律,可判断最后结果的个位数字.
解答 解:原式=(22-1)(22+1)(24+1)…(232+1)+2=(24-1)(24+1)…(232+1)+1=264-1+1=264,
∵2的指数是1时,个位是2;2的指数是2时,个位是4;2的指数是3时,个位是8;2的指数是4时,个位是6;
64是4的倍数,
∴264的个位是6.
故选:C.
点评 本题考查了平方差公式、有理数的乘方.解题的关键是知道2+1=22-1,以及2的任何次方幂的个位数字的规律.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
8.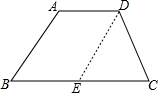 如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )
如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )
 如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )
如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )| A. | AB∥DE且AB=DE | B. | ∠DEC=∠B | C. | AD∥EC且AD=EC | D. | BC=AD+EC |
10.计算(-x+2y)2的结果是( )
| A. | -x2+2y2 | B. | -2x+4y | C. | 4y2-x2 | D. | x2-4xy+4y2 |
7.代数式$\frac{1}{\sqrt{x-2}}$有意义的x取值范围是( )
| A. | x≥2 | B. | x>2 | C. | x≠2 | D. | x<2 |
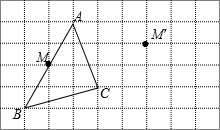 (1)如图,点M是△ABC中AB的中点,经平移后,点M落在M′处.请在正方形网格中画出△ABC平移后的图形△A′B′C′.
(1)如图,点M是△ABC中AB的中点,经平移后,点M落在M′处.请在正方形网格中画出△ABC平移后的图形△A′B′C′. 如图,MN∥BC,∠AEN=100°,∠B=65°,则∠A=35°.
如图,MN∥BC,∠AEN=100°,∠B=65°,则∠A=35°.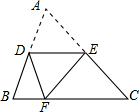 如图,将三角形ABC沿着DE折叠,使点A落在BC上的点F处,且DE∥BC,若∠B=65°,则∠BDF=50°.
如图,将三角形ABC沿着DE折叠,使点A落在BC上的点F处,且DE∥BC,若∠B=65°,则∠BDF=50°.