题目内容
19.已知$x=\sqrt{5}-3$,求代数式$\frac{x-3}{x-2}÷(x+2-\frac{5}{x-2})$的值.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{x-3}{x-2}$÷$\frac{{x}^{2}-9}{x-2}$
=$\frac{x-3}{x-2}$•$\frac{x-2}{(x+3)(x-3)}$
=$\frac{1}{x+3}$,
当x=$\sqrt{5}$-3时,原式=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.计算(-x+2y)2的结果是( )
| A. | -x2+2y2 | B. | -2x+4y | C. | 4y2-x2 | D. | x2-4xy+4y2 |
7.代数式$\frac{1}{\sqrt{x-2}}$有意义的x取值范围是( )
| A. | x≥2 | B. | x>2 | C. | x≠2 | D. | x<2 |
4.(-0.5)2的平方根是( )
| A. | -0.5 | B. | ±0.5 | C. | 0.5 | D. | 0.25 |
11.在等式a3•a2•( )=a11中,括号里面的代数式是( )
| A. | a7 | B. | a8 | C. | a6 | D. | a3 |
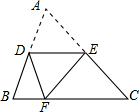 如图,将三角形ABC沿着DE折叠,使点A落在BC上的点F处,且DE∥BC,若∠B=65°,则∠BDF=50°.
如图,将三角形ABC沿着DE折叠,使点A落在BC上的点F处,且DE∥BC,若∠B=65°,则∠BDF=50°.