如图.设四边形ABCD是边长为1的正方形.以对角线AC为边作第2个正方形ACEF.再以对角线AE为边作第3个正方形AEGH.如此下去-.记正方形ABCD的面积S1=1.按上述方法所作的正方形的面积依次为S2.S3-.Sn.则Sn=( )A．2n-1B．2nC．2n+1D．2n+2 题目和参考答案——青夏教育精英家教网—

题目内容

17．

如图，设四边形ABCD是边长为1的正方形，以对角线AC为边作第2个正方形ACEF，再以对角线AE为边作第3个正方形AEGH，如此下去…，记正方形ABCD的面积S₁=1，按上述方法所作的正方形的面积依次为S₂，S₃…，S_n，则S_n=（　　）

A．

2^n-1

B．

2ⁿ

C．

2ⁿ⁺¹

D．

2ⁿ⁺²

分析根据正方形的性质易得：正方形的对角线是正方形的边长的$\sqrt{2}$倍；进而根据题意，找到第二个正方形与第一个正方形面积的关系，依此类推，可得第n个正方形S_n的面积．

解答解：根据勾股定理得：正方形的对角线是正方形的边长的$\sqrt{2}$倍；
即第二个正方形的面积是第一个正方形面积的2倍，即是2，…
依此类推第n个正方形的面积是上一个正方形面积的2倍，即2×2×2…×2（n-1个2）=2^n-1．
故选A

点评本题考查正方形的性质，要求学生能够根据勾股定理得到前后正方形的边长之间的关系，进一步得到面积之间的关系．从而找到规律．

练习册系列答案

课标新卷系列答案

课时练测试卷系列答案

小考冲刺金卷系列答案

初中学业水平考试总复习专项复习卷加全真模拟卷系列答案

相关题目

7．

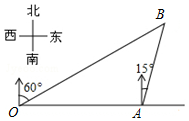如图，港口A在观测站O的正东方向，OA=6km，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离（即AB的长）为（　　）

8．我市10月的某周七天的最高气温（单位：℃）统计如下：19，20，24，22，24，26，27，则这组数据的中位数与众数分别是（　　）

5．

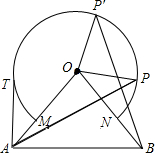如图，△OAB中，OA=OB=10，∠AOB=70°，以点O为圆心，6为半径的优弧$\widehat{MN}$分别交OA、OB于点M，N．
（1）点P在右半弧上（∠BOP是锐角），将OP绕点O逆时针旋转70°得OP′．求证：AP=BP′；
（2）点T在左半弧上，若AT与弧相切，求点T到OA的距离；
（3）设点Q在优弧$\widehat{MN}$上，当△AOQ的面积最大时，直接写出∠BOQ的度数．

12．已知抛物线y=-x²+2x+2，该抛物线的对称轴是直线x=1，顶点坐标（1，3）．

2．若n满足（n-1）ⁿ⁺²=1，则整数n的值是-2，0，2．

9．

如图，已知AE，BD是△ABC的角平分线，AE与BD相交于点P，若AB=BC，且AB≠AC，则图中的全等三角形有（　　）

6．

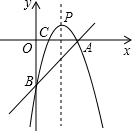如图，直线y=x-3与x轴、y轴分别相交于点A，B，经过A，B两点的抛物线y=-x²+bx+c与x轴的另一个交点为C．
（1）确定抛物线的解析式及点C的坐标；
（2）在抛物线的对称轴上是否存在点E，使得EB+EC的值最小，若存在，求出点E的坐标；若不存在，请说明理由；
（3）在抛物线上是否存在点F，连接AF，使∠FAO=∠OBC，若存在，求出点F的坐标；若不存在，请说明理由．

7．

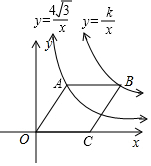如图，点A在双曲线y=$\frac{4\sqrt{3}}{x}$（x＞0）上，点B在双曲线y=$\frac{k}{x}$上，（点B在点A的右侧），且AB∥x轴，若四边形OABC是菱形，且∠AOC=60°，则k=12$\sqrt{3}$．

试题分类