题目内容
12.已知抛物线y=-x2+2x+2,该抛物线的对称轴是直线x=1,顶点坐标(1,3).分析 把抛物线解析式化为顶点式可求得答案.
解答 解:
∵y=-x2+2x+2=-(x-1)2+3,
∴抛物线对称轴为x=1,顶点坐标为(1,3),
故答案为:直线x=1;(1,3).
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,对称轴为直线x=h,顶点坐标为(h,k).

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
7.已知抛物线y=ax2+bx+c的对称轴是x=2,且经过点(1,0),则9a+3b+c的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 3 |
17. 如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第2个正方形ACEF,再以对角线AE为边作第3个正方形AEGH,如此下去…,记正方形ABCD的面积S1=1,按上述方法所作的正方形的面积依次为S2,S3…,Sn,则Sn=( )
如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第2个正方形ACEF,再以对角线AE为边作第3个正方形AEGH,如此下去…,记正方形ABCD的面积S1=1,按上述方法所作的正方形的面积依次为S2,S3…,Sn,则Sn=( )
 如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第2个正方形ACEF,再以对角线AE为边作第3个正方形AEGH,如此下去…,记正方形ABCD的面积S1=1,按上述方法所作的正方形的面积依次为S2,S3…,Sn,则Sn=( )
如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第2个正方形ACEF,再以对角线AE为边作第3个正方形AEGH,如此下去…,记正方形ABCD的面积S1=1,按上述方法所作的正方形的面积依次为S2,S3…,Sn,则Sn=( )| A. | 2n-1 | B. | 2n | C. | 2n+1 | D. | 2n+2 |
2.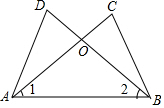 如图,AC、BD相交于点O,∠1=∠2,若用“SAS”说明△ACB≌△BDA,则还需要加上条件( )
如图,AC、BD相交于点O,∠1=∠2,若用“SAS”说明△ACB≌△BDA,则还需要加上条件( )
 如图,AC、BD相交于点O,∠1=∠2,若用“SAS”说明△ACB≌△BDA,则还需要加上条件( )
如图,AC、BD相交于点O,∠1=∠2,若用“SAS”说明△ACB≌△BDA,则还需要加上条件( )| A. | AD=BC | B. | BD=AC | C. | ∠D=∠C | D. | OA=AB |
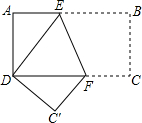 在长方形纸片ABCD中,AD=6cm,AB=8cm,按如图方式折叠,使点B与点D重合,折痕为EF,则EF的长为$\frac{15}{2}$.
在长方形纸片ABCD中,AD=6cm,AB=8cm,按如图方式折叠,使点B与点D重合,折痕为EF,则EF的长为$\frac{15}{2}$. 在平面直角坐标系中,?ABOC如图放置,点C的坐标是(-1,0),点A在y轴的正半轴上,将此平行四边形绕点O顺时针旋转90°,得?A′B′OC′,抛物线y=ax2+bx+4过点C、A、A′,点M是此抛物线的一动点,设点M的横坐标为m.
在平面直角坐标系中,?ABOC如图放置,点C的坐标是(-1,0),点A在y轴的正半轴上,将此平行四边形绕点O顺时针旋转90°,得?A′B′OC′,抛物线y=ax2+bx+4过点C、A、A′,点M是此抛物线的一动点,设点M的横坐标为m.