题目内容
18. 如图,矩形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD于点E.
如图,矩形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD于点E.(1)求证:∠BAM=∠AEF;
(2)若AB=4,AD=6,cos∠BAM=$\frac{4}{5}$,求DE的长.
分析 (1)由矩形的性质以及垂直的性质可得∠BAM+∠EAF=∠AEF+∠EAF=90°,进而可证明∠BAM=∠AEF;
(2)在直角三角形AEF中,利用已知条件可求出AE的长,因为AD的长已知,所以DE的长可用求出.
解答 解:(1)∵四边形ABCD是矩形,
∴∠B=∠BAC=90°.
∵EF⊥AM,
∴∠AFE=∠B=∠BAD=90°.
∴∠BAM+∠EAF=∠AEF+∠EAF=90°.
∴∠BAM=∠AEF;
(2)在Rt△ABM中,∠B=90°,AB=4,cos∠BAM=$\frac{4}{5}$,
∴AM=5.
∵F为AM中点,
∴AF=2.5,
∵∠BAM=∠AEF,
∴cos∠BAM=cos∠AEF=$\frac{4}{5}$.
∴sin∠AEF=$\frac{3}{5}$.
在Rt△AEF中,
∠AFE=90°,AF=$\frac{5}{2}$,sin∠AEF=$\frac{3}{5}$,
∴AE=$\frac{25}{6}$.
∴DE=AD-AE=6-$\frac{25}{6}$=$\frac{11}{6}$.
点评 此题主要考查了锐角三角函数的关系以及矩形的性质,根据已知得出sin∠AEF的值是解题关键.

练习册系列答案
相关题目
9.下列命题中的真命题是( )
| A. | 两直线平行,同旁内角相等 | |
| B. | 同位角互补,两直线平行 | |
| C. | 三角形的外角等于它的两个内角的和 | |
| D. | 锐角三角形的内角和等于钝角三角形的内角和 |
 如图,等边△ABC及其内切圆与外接圆构成的图形中,若外接圆的半径为3,则图中阴影部分的面积为3π.
如图,等边△ABC及其内切圆与外接圆构成的图形中,若外接圆的半径为3,则图中阴影部分的面积为3π.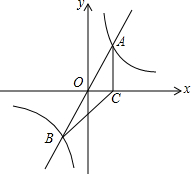 如图,正比例函数y=mx的图象与双曲线y=$\frac{k}{x}$相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.
如图,正比例函数y=mx的图象与双曲线y=$\frac{k}{x}$相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC. 如图,双曲线y=$\frac{k}{x}$与直线y=x+1相交于A、B两点,点A的纵坐标为2
如图,双曲线y=$\frac{k}{x}$与直线y=x+1相交于A、B两点,点A的纵坐标为2 将长方形ABCD沿AE折叠,得到如图所示的图形,已知∠CEB′=$\frac{2}{5}$∠AEB′,则∠AEB′=75°.
将长方形ABCD沿AE折叠,得到如图所示的图形,已知∠CEB′=$\frac{2}{5}$∠AEB′,则∠AEB′=75°.