Question

8．如图，等边△ABC及其内切圆与外接圆构成的图形中，若外接圆的半径为3，则图中阴影部分的面积为3π．

Answer 1

分析 由等边三角形和圆的轴对称性可知：阴影部分的面积等于圆心角是120°的扇形的面积，代入数值求出即可．

解答 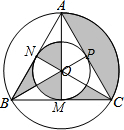解：∵△ABC是等边三角形，大⊙O是△ABC的外切圆，
∴AO=OB=OC，
∵小⊙O是△ABC的内切圆，
∴OM=ON=OP，
∴∠AOC=120°，∠AON=∠BON=∠AOP=∠CON=60°，
BN=CM=AP=CP，
∴S_阴影=S_扇形AOC=$\frac{120•π×{3}^{2}}{360}$=3π，
故答案为：3π．

点评 本题考查了三角形的内切圆与内心，等边三角形的性质，扇形的面积计算，三角形的外切圆和外心，把各个阴影部分拼成一个扇形是解题的关键．