题目内容
17. 如图,△ABC中,D、E分别是AB、AC的中点.求证:DE=$\frac{1}{2}$BC,DE∥BC.
如图,△ABC中,D、E分别是AB、AC的中点.求证:DE=$\frac{1}{2}$BC,DE∥BC.
分析 延长DE至F,使EF=DE,连接FC,证明△AED≌△CEF,根据平行四边形的判定定理证明四边形DBCF是平行四边形,根据平行四边形的性质证明结论.
解答 证明: 延长DE至F,使EF=DE,连接FC,
延长DE至F,使EF=DE,连接FC,
在△AED和△CEF中,
$\left\{\begin{array}{l}{AE=EC}\\{∠AED=∠CEF}\\{DE=EF}\end{array}\right.$,
∴△AED≌△CEF,
∴∠A=∠ECF,AD=CF,
∴AB∥CF,FC=BD,
∴四边形DBCF是平行四边形,
∴DE∥BC,DF=BC,
∵DE=$\frac{1}{2}$DF,
∴DE=$\frac{1}{2}$BC,
∴DE=$\frac{1}{2}$BC,DE∥BC.
点评 本题考查的是三角形中位线定理的证明,掌握平行四边形的判定定理和性质定理是解题的关键,注意辅助线的作法要正确.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
7.下面四个图案中,不能由基本图案旋转得到的是( )
| A. |  | B. |  | C. |  | D. |  |
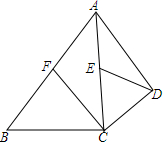 如图,在四边形ABCD中,$\frac{BC}{CD}$=$\frac{3}{2}$,AC平分∠BAD,∠ACB=∠ADC=90°,CF和DE是△ABC、△ACD的中线,求$\frac{CE}{DE}$的值.
如图,在四边形ABCD中,$\frac{BC}{CD}$=$\frac{3}{2}$,AC平分∠BAD,∠ACB=∠ADC=90°,CF和DE是△ABC、△ACD的中线,求$\frac{CE}{DE}$的值.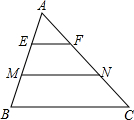 已知:如图,E、M是AB边的三等分点,EF∥MN∥BC.求:△AEF的面积:四边形EMNF的面积:四边形MBCN的面积.
已知:如图,E、M是AB边的三等分点,EF∥MN∥BC.求:△AEF的面积:四边形EMNF的面积:四边形MBCN的面积.