题目内容
12.四个数a、b、c、d排成2行、2列,两边各加一条竖直线记成$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$,定义$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,这个记号就叫做2阶行列式.例如:$|\begin{array}{l}{1}&{2}\\{3}&{4}\end{array}|$=1×4-2×3=-2.若$|\begin{array}{l}{x+1}&{x+2}\\{x-2}&{x+1}\end{array}|$=10,求x的值.分析 已知等式利用题中的新定义化简,计算即可求出x的值.
解答 解:已知等式利用题中的新定义整理得:(x+1)2-(x+2)(x-2)=10,
整理得:x2+2x+1-x2+4=10,
解得:x=$\frac{5}{2}$.
点评 此题考查了多项式乘多项式,以及解一元一次方程,弄清题中的新定义是解本题的关键.

练习册系列答案
相关题目
17.在实数π,2,0,3.14,-$\sqrt{2}$,tan45°,3.1415926,$\frac{1}{7}$,1.010010001…(每两个1之间0的个数依次加1)中,无理数的个数是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.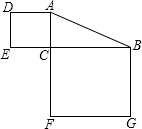 如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
 如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )| A. | 150 | B. | 200 | C. | 225 | D. | 无法比较 |
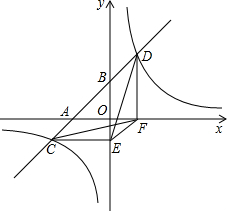 如图,直线l与x轴、y轴交于A、B两点.与双曲线y=$\frac{k}{x}$和交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F.连接CF、DE.则下列结论中:
如图,直线l与x轴、y轴交于A、B两点.与双曲线y=$\frac{k}{x}$和交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F.连接CF、DE.则下列结论中:
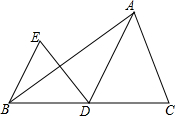 如图,AD是△ABC中BC边上的中线,∠ADC为锐角,把△ADC沿直线AD折过来,点C落在点E的位置上.试猜想直线BE与直线DA的位置关系,并证明你的猜测.
如图,AD是△ABC中BC边上的中线,∠ADC为锐角,把△ADC沿直线AD折过来,点C落在点E的位置上.试猜想直线BE与直线DA的位置关系,并证明你的猜测.