题目内容
1.若△ABC的面积为8,则它的三条中位线所围成的三角形的面积是2.分析 根据三角形中位线定理即可证得:$\frac{DE}{BC}$=$\frac{FE}{AB}$=$\frac{DF}{AC}$=$\frac{1}{2}$,则△DEF∽△ABC,根据相似三角形的面积的比等于相似比的平方即可求解.
解答 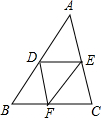 解:∵DE是△ABC的中位线,
解:∵DE是△ABC的中位线,
∴DE=$\frac{1}{2}$BC,即$\frac{DE}{BC}$=$\frac{1}{2}$,
同理,$\frac{FE}{AB}$=$\frac{1}{2}$,$\frac{DF}{AC}$=$\frac{1}{2}$,
∴$\frac{DE}{BC}$=$\frac{FE}{AB}$=$\frac{DF}{AC}$=$\frac{1}{2}$,
∴△DEF∽△ABC,
∴$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=$\frac{1}{4}$,
∴S△DEF=$\frac{1}{4}$S△ABC=$\frac{1}{4}$×8=2.
故答案是:2.
点评 本题考查了三角形的中位线定理,以及相似三角形的性质,正确证明△DEF∽△ABC是关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
6.某班有35位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于23人.”乙说:“两项都参加的人数小于11.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是( )
| A. | 若甲对,则乙对 | B. | 若甲错,则乙对 | C. | 若乙对,则甲对 | D. | 若乙错,则甲错 |
11.据统计,长春市主城区2015年上半年机动车数量突破1000000辆大关,1000000这个数用科学记数法表示为( )
| A. | 1×107 | B. | 0.1×107 | C. | 1×106 | D. | 10×101 |
 写出如图表示的不等式的解集是x≤1.
写出如图表示的不等式的解集是x≤1.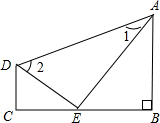 如图,AE平分∠BAD,DE平分∠ADC,AB⊥BC于B,∠1+∠2=90°,试判断DC与BC的位置关系,并加以说明.
如图,AE平分∠BAD,DE平分∠ADC,AB⊥BC于B,∠1+∠2=90°,试判断DC与BC的位置关系,并加以说明.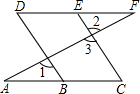 如图,若∠1=∠2,∠C=∠D,问∠A与∠F有什么关系?并说明理由.
如图,若∠1=∠2,∠C=∠D,问∠A与∠F有什么关系?并说明理由.