题目内容
18.关于x的代数式(3-ax)(x2+2x-1)的展开式中不含x2项,则a=$\frac{3}{2}$.分析 原式利用多项式乘以多项式法则计算,合并后根据展开式中不含x2项,求出a的值即可.
解答 解:(3-ax)(x2+2x-1)=(3-2a)x2+(a+6)x-3-ax3,
由展开式中不含x2项,得到3-2a=0,
解得:a=$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 此题考查了多项式乘以多项式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
3.一次函数y=kx+b与反比例函数y=$\frac{m}{x}$中,若x与y的部分对应值如表:
则关于x的不等式$\frac{m}{x}$≤kx+b的解集是x≤-1或0<x≤3.
| x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
| y=kx+b | … | 5 | 4 | 3 | 1 | 0 | -1 | … |
| y=$\frac{m}{x}$ | … | 1 | $\frac{3}{2}$ | 3 | -3 | -$\frac{3}{2}$ | -1 | … |
7.下列调査中,适合采用全面调査(普査)方式的是( )
| A. | 调査某池塘中现有鱼的数量 | |
| B. | 对端午节期间市场上粽子质量情况的调査 | |
| C. | 企业招聘,对应聘人员进行面试 | |
| D. | 对某类烟花爆竹燃放安全情况的调査 |
 如图,将三角尺的直角顶点放在直线a上,a∥b,∠1=50°,∠2=60°,则∠3的度数为70°.
如图,将三角尺的直角顶点放在直线a上,a∥b,∠1=50°,∠2=60°,则∠3的度数为70°.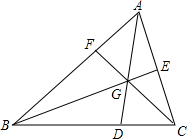 如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,AD,BE,CF交于一点G,BC=3DC,S△GEC=3,S△GBD=8,则△ABC的面积是30.
如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,AD,BE,CF交于一点G,BC=3DC,S△GEC=3,S△GBD=8,则△ABC的面积是30.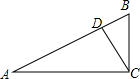 如图,在△ABC中,∠ACB=90°,D为AB边上一点,∠BCD=35°,∠BDC=80°.求∠A的度数.
如图,在△ABC中,∠ACB=90°,D为AB边上一点,∠BCD=35°,∠BDC=80°.求∠A的度数.