题目内容
9．不改变分式的值，使分式分子与分母中最高次项的系数是正数，并把分子与分母中的多项式按x降幂排列．（1）$\frac{2x+1-{x}^{2}}{-3-2x}$；
（2）-$\frac{{x}^{3}-3x+1}{2-{x}^{2}}$．
分析 （1）让分子，分母同时乘以-1可让分子和分母中x的最高次项的系数都是正数；
（2）根据分式的分子、分母、分式改变任意两项的符号，分式的值不变，可得答案．
解答 解：（1）$\frac{2x+1-{x}^{2}}{-3-2x}$=$\frac{{x}^{2}-2x-1}{2x+3}$；
（2）-$\frac{{x}^{3}-3x+1}{2-{x}^{2}}$=$\frac{{x}^{3}-3x+1}{{x}^{2}-2}$．
点评 本题考查了分式的基本性质，利用分式的基本性质是解答此题的关键．
练习册系列答案
寒假学与练系列答案
相关题目
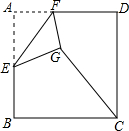如图，在边长为2的正方形ABCD中，E是AB的中点，F是AD边上的一个动点，将△AEF沿EF所在直线折叠得到△GEF，连接GC，则GC长度的最小值是$\sqrt{5}$-1．
将一副三角板按如图放置，则下列结论①∠1=∠3；②如果∠2=30°则有AC∥DE；③如果∠2=30°，则有BC∥AD；④如果∠2=30°，必有∠4=∠C，其中正确的有（ ）