题目内容
11.已知抛物线y=x2-2x-3与y轴交于C点,与x轴交于A、B两点,求直线BC的函数表达式.分析 由抛物线可求得A、B、C的坐标,再根据待定系数法可求得BC的函数解析式.
解答 解:
在y=x2-2x-3中,令y=0可得x2-2x-3=0,解得x=3或x=-1,
∴A、B两点的坐标为(3,0)和(-1,0),
在y=x2-2x-3中,令x=0可得y=-3,
∴C点坐标为(0,-3),
设直线BC解析式为y=kx+b,
当B点坐标为(3,0)时,
把B、C两点坐标代入可得$\left\{\begin{array}{l}{b=-3}\\{3k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$,
∴直线BC的解析式为y=x-3;
当B点坐标为(-1,0)时,
把B、C两点坐标代入可得$\left\{\begin{array}{l}{b=-3}\\{-k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-3}\\{b=-3}\end{array}\right.$,
∴直线BC的解析式为y=-3x-3;
综上可知直线BC的解析式为y=x-3或y=-3x-3.
点评 本题主要考查待定系数法求函数解析式,由抛物线解析式确定出A、B、C三点的坐标是解题的关键,注意分两种情况.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
20.能够构成平行四边形三个内角的度数是( )
| A. | 85°,95°,85° | B. | 85°,105°,75° | C. | 85°,85°,115° | D. | 85°,95°,105° |
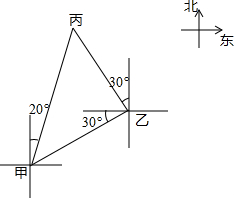 如图所示,有甲、乙、丙三个村庄,已知丙村在乙村北偏西30°方向,丙村在甲村北偏东20°方向,甲村在乙村西偏南30°方向,现要从甲村分别向乙村、丙村各修一条公路,则这两条公路应成多少度角?
如图所示,有甲、乙、丙三个村庄,已知丙村在乙村北偏西30°方向,丙村在甲村北偏东20°方向,甲村在乙村西偏南30°方向,现要从甲村分别向乙村、丙村各修一条公路,则这两条公路应成多少度角?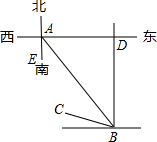 如图,小张从家(图中A处)出发,向南偏东40°的方向走到学校(图中B处)再从学校出发,向北偏西75°的方向走到小明家(图中C处),则∠ABC为35度.
如图,小张从家(图中A处)出发,向南偏东40°的方向走到学校(图中B处)再从学校出发,向北偏西75°的方向走到小明家(图中C处),则∠ABC为35度.