题目内容
10.解关于x,y的方程组$\left\{\begin{array}{l}{x+y+z=26}\\{2x-y+z=18}\end{array}\right.$,并求出x-y=1时z的值.分析 将z看做已知常数消元法求解可得,再将x、y代入到x-y=1可得18-$\frac{2}{3}$z-$\frac{34-z}{3}$=1,解之可得.
解答 解:$\left\{\begin{array}{l}{x+y=26-z}&{①}\\{2x-y=18-z}&{②}\end{array}\right.$,
①+②,得:3x=54-2z,
∴x=18-$\frac{2}{3}$z,
①×2-②,得:y=$\frac{34-z}{3}$,
∴方程组的解为$\left\{\begin{array}{l}{x=18-\frac{2}{3}z}\\{y=\frac{34-z}{3}}\end{array}\right.$;
∵x-y=1,
∴18-$\frac{2}{3}$z-$\frac{34-z}{3}$=1,
解得:z=17.
点评 本题主要考查解二元一次方程组和解一元一次方程的能力,熟练掌握消元法解方程组和解一元一次方程的基本步骤是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列正确的是( )
| A. | 若ac=bc,则a=b | B. | 若$\frac{a}{c}$=$\frac{b}{c}$,则a=b | C. | 若a2=b2,则a=b | D. | 若|a|=|b|,则a=b |
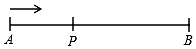 如图,已知舞台AB长10米,如果报幕员从点A出发站在舞台的黄金分割点P处,且AP<BP,则报幕员应走3.8 米报幕(结果精确到0.1米).
如图,已知舞台AB长10米,如果报幕员从点A出发站在舞台的黄金分割点P处,且AP<BP,则报幕员应走3.8 米报幕(结果精确到0.1米).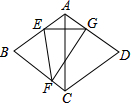 如图,在菱形ABCD中,∠BAD=120°,点E,F分别在AB,BC上,将△BEF沿EF折叠,点B落在AD上的点G处,EG⊥AC.
如图,在菱形ABCD中,∠BAD=120°,点E,F分别在AB,BC上,将△BEF沿EF折叠,点B落在AD上的点G处,EG⊥AC.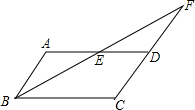 如图,在?ABCD中,点E是AD的中点,BE的延长线与CD的延长线相交于点F.
如图,在?ABCD中,点E是AD的中点,BE的延长线与CD的延长线相交于点F.