题目内容
1.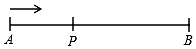 如图,已知舞台AB长10米,如果报幕员从点A出发站在舞台的黄金分割点P处,且AP<BP,则报幕员应走3.8 米报幕(结果精确到0.1米).
如图,已知舞台AB长10米,如果报幕员从点A出发站在舞台的黄金分割点P处,且AP<BP,则报幕员应走3.8 米报幕(结果精确到0.1米).
分析 根据黄金分割的定义,先求出PB=$\frac{\sqrt{5}-1}{2}$AB,再根据AP=AB-PB计算即可得解.
解答 解:∵点P为AB的黄金分割点,AP<BP,
∴PB=$\frac{\sqrt{5}-1}{2}$AB=$\frac{\sqrt{5}-1}{2}$×10=5$\sqrt{5}$-5(米),
∴AP=AB-PB=10-(5$\sqrt{5}$-5)=15-5$\sqrt{5}$≈3.8(米).
故答案为:3.8.
点评 本题考查了黄金分割的应用.关键是明确黄金分割所涉及的线段的比.也考查了近似数和有效数字.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若|a|=-a,则a为( )
| A. | 正数 | B. | 0和正数 | C. | 负数 | D. | 0和负数 |
9.y=x2-2x-3的顶点坐标和对称轴( )
| A. | (-1,-4),直线x=-1 | B. | (1,-4),直线x=1 | C. | (-1,4),直线x=-1 | D. | (1,4),直线x=1 |
11.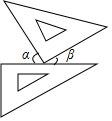 把一副三角板按如图方式的位置摆放,则形成两个角,设分别是∠α,∠β,若∠α=55°,则∠β=( )
把一副三角板按如图方式的位置摆放,则形成两个角,设分别是∠α,∠β,若∠α=55°,则∠β=( )
 把一副三角板按如图方式的位置摆放,则形成两个角,设分别是∠α,∠β,若∠α=55°,则∠β=( )
把一副三角板按如图方式的位置摆放,则形成两个角,设分别是∠α,∠β,若∠α=55°,则∠β=( )| A. | 25° | B. | 35° | C. | 45° | D. | 55° |
 如图是一个正方体的表面展开图,每个面上都标注了字母,请根据要求回答下列问题:
如图是一个正方体的表面展开图,每个面上都标注了字母,请根据要求回答下列问题: