题目内容
5.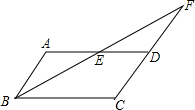 如图,在?ABCD中,点E是AD的中点,BE的延长线与CD的延长线相交于点F.
如图,在?ABCD中,点E是AD的中点,BE的延长线与CD的延长线相交于点F.(1)求证:DE是△BCF的中位线.
(2)试连接BD,AF,判断四边形ABDF的形状,并证明你的结论.
分析 (1)由平行四边形的性质即可证明DE是△BCF的中位线;
(2)因为平行四边形的对边平行且相等,所以AB∥CD,AB=CD;又因为点E是AD的中点,易得△ABE≌△DFE,所以AB=DF,所以四边形ABDF为平行四边形.
解答 解:
(1)∵四边形ABCD是平行四边形,
∴DE∥BC,
∴点E是AD的中点,
∴DF=CD,
∴DE是△BCF的中位线;
(2)四边形ABDF为平行四边形,
理由:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠ABE=∠BFD,
∵点E是AD的中点,
∴AE=DE,
∵∠AEB=∠DEF,
∴△ABE≌△DFE,
∴AB=DF,
∵AB∥DF,
∴四边形ABDF为平行四边形
点评 此题考查了平行四边形的性质:平行四边形的对边平行且相等.此题还考查了平行四边形的判定:一组对边平行且相等的四边形是平行四边形.解题的关键是准确选择适宜的判定方法.

练习册系列答案
相关题目
14.西安铁一中滨河学校为了提高五人小组合作热情并促进学生平时对各科核心知识的落实,自建校以来有一个教学特色即每周每天随机从各班选一个小组进行一科的抽检.已知初二一数学老师所带班级的两个小组共10名学生的一次数学抽检成绩平均分是73分,设这个班10名学生抽检成绩的中位数为b分,下表是具体分数统计表:
则x,b的值分别是( )
| 成绩(分) | 50 | 60 | 70 | 80 | 90 |
| 人数(人) | 1 | 2 | x | y | 2 |
| A. | 3,70 | B. | 3,75 | C. | 2,70 | D. | 2,75 |