题目内容
10.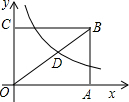 如图,已知矩形OABC面积为$\frac{100}{3}$,它的对角线OB与双曲线$y=\frac{k}{x}$相交于D且OB:OD=5:3,则k=( )
如图,已知矩形OABC面积为$\frac{100}{3}$,它的对角线OB与双曲线$y=\frac{k}{x}$相交于D且OB:OD=5:3,则k=( )| A. | 6 | B. | 12 | C. | 24 | D. | 36 |
分析 先找到点的坐标,然后再利用矩形面积公式计算,确定k的值.
解答 解:由题意,设点D的坐标为(xD,yD),
则点B的坐标为($\frac{5}{3}$xD,$\frac{5}{3}$yD),
矩形OABC的面积=|$\frac{5}{3}$xD×$\frac{5}{3}$yD|=$\frac{100}{3}$,
∵图象在第一象限,
∴k=xD•yD=12.
故选B.
点评 本题考查了反比例函数与几何图形的结合,综合性较强,同学们应重点掌握.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
5.在Rt△ABC中,∠C=90°,BC=5,CA=12,则cosB=( )
| A. | $\frac{5}{12}$ | B. | $\frac{12}{5}$ | C. | $\frac{5}{13}$ | D. | $\frac{12}{13}$ |
2.(2a+3b)2=(2a-3b)2+ ,横线上应填的式子是( )
| A. | 6ab | B. | 24ab | C. | 12ab | D. | 18ab |
19.n边形的内角和等于外角和的2倍,则n的值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
20.若a=-0.32,b=-3-2,c=(-$\frac{1}{3}$)-2,d=(-$\frac{1}{5}$)0,则a、b、c、d大小关系正确的是( )
| A. | a<b<c<d | B. | b<a<d<c | C. | a<d<c<b | D. | a<b<d<c |
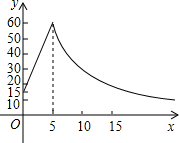 如图所示,制作一种产品的同时,需要将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟,据了解,该材料在加热过程中温度y与时间x成一次函数关系,已知该材料在加热前的温度为15℃,加热5分钟使材料温度达到60℃时停止加热.停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系.
如图所示,制作一种产品的同时,需要将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟,据了解,该材料在加热过程中温度y与时间x成一次函数关系,已知该材料在加热前的温度为15℃,加热5分钟使材料温度达到60℃时停止加热.停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系.