题目内容
1.α、β是关于x的方程4x2-4mx+m2+4m=0的两个实根,并且满足(α-1)(β-1)=2,求m的值.分析 先根据一元二次方程根与系数的关系求出α+β与αβ,再代入(α-1)(β-1)=2求出m的值,然后用根的判别式进行检验.
解答 解∵α、β是关于x的方程4x2-4mx+m2+4m=0的两个实根,
∴α+β=m,αβ=$\frac{{m}^{2}+4m}{4}$,
∵(α-1)(β-1)=2,
∴αβ-(α+β)+1=2,
即:$\frac{{m}^{2}+4m}{4}$-m=1,
化简得:m2=4,
故m=±2,
又∵△=16m2-16m2-64m≥0,
解得:m≤0,
∴m=-2.
点评 本题考查了根的判别式,根与系数的关系,属于基础题,关键是要熟记x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.如果分式$\frac{{x}^{2}-4}{{x}^{2}-3x+2}$的值为零,那么x等于( )
| A. | -2 | B. | 2 | C. | -2或2 | D. | 1或2 |
13.若x是不为0的有理数,已知M=(x2+1)(x2-1),N=(x2+1)2,则M与N的大小关系是( )
| A. | M>N | B. | M<N | C. | M=N | D. | 无法确定 |
11. 如图,两个正方形边长分别为a、b,a+b=16,ab=48,图中阴影部分的面积为( )
如图,两个正方形边长分别为a、b,a+b=16,ab=48,图中阴影部分的面积为( )
 如图,两个正方形边长分别为a、b,a+b=16,ab=48,图中阴影部分的面积为( )
如图,两个正方形边长分别为a、b,a+b=16,ab=48,图中阴影部分的面积为( )| A. | 56 | B. | 72 | C. | 80 | D. | 104 |
 如图,边长为1的小正方形构成的网格中,半径为1的⊙O在格点上,则∠AED的正切值为$\frac{1}{2}$.
如图,边长为1的小正方形构成的网格中,半径为1的⊙O在格点上,则∠AED的正切值为$\frac{1}{2}$. 如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=6,EF=8,则边AD的长是10.
如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=6,EF=8,则边AD的长是10.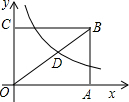 如图,已知矩形OABC面积为$\frac{100}{3}$,它的对角线OB与双曲线$y=\frac{k}{x}$相交于D且OB:OD=5:3,则k=( )
如图,已知矩形OABC面积为$\frac{100}{3}$,它的对角线OB与双曲线$y=\frac{k}{x}$相交于D且OB:OD=5:3,则k=( )