题目内容
7.已知关于x的一元二次方程x2-4x+m=0.(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根为x1,x2,且满足5x1+2x2=2,求实数m的值.
分析 (1)若一元二次方程有两实数根,则根的判别式△=b2-4ac≥0,建立关于m的不等式,求出m的取值范围;
(2)根据根与系数的关系得到x1+x2=4,又5x1+2x2=2求出函数实数根,代入m=x1x2,即可得到结果.
解答 解:(1)∵方程有实数根,
∴△=(-4)2-4m=16-4m≥0,
∴m≤4;
(2)∵x1+x2=4,
∴5x1+2x2=2(x1+x2)+3x1=2×4+3x1=2,
∴x1=-2,
把x1=-2代入x2-4x+m=0得:(-2)2-4×(-2)+m=0,
解得:m=-12.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程根与系数的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.某合作学习小组的6名同学在一次数学测试中,成绩分布为76,88,96,82,78,96,这组数据的中位数是( )
| A. | 82 | B. | 85 | C. | 88 | D. | 96 |
12.某种细胞的直径是0.000067厘米,将0.000067用科学记数法表示为( )
| A. | 6.7×10-5 | B. | 0.67×10-6 | C. | 0.67×10-5 | D. | 6.7×10-6 |
 如图,边长为1的小正方形构成的网格中,半径为1的⊙O在格点上,则∠AED的正切值为$\frac{1}{2}$.
如图,边长为1的小正方形构成的网格中,半径为1的⊙O在格点上,则∠AED的正切值为$\frac{1}{2}$. 如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=6,EF=8,则边AD的长是10.
如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=6,EF=8,则边AD的长是10.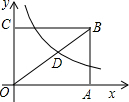 如图,已知矩形OABC面积为$\frac{100}{3}$,它的对角线OB与双曲线$y=\frac{k}{x}$相交于D且OB:OD=5:3,则k=( )
如图,已知矩形OABC面积为$\frac{100}{3}$,它的对角线OB与双曲线$y=\frac{k}{x}$相交于D且OB:OD=5:3,则k=( )