题目内容
2.(2a+3b)2=(2a-3b)2+ ,横线上应填的式子是( )| A. | 6ab | B. | 24ab | C. | 12ab | D. | 18ab |
分析 先移项,再利用平方差公式将(2a+3b)2-(2a-3b)2展开即可得到答案.
解答 解:设横线上应填的式子是M,
则有M=(2a+3b)2-(2a-3b)2=(2a+3b-2a+3b)(2a+3b+2a-3b)=6b•4a=24ab,
所以横线上的式子是24ab,
故选:B.
点评 本题考查了平方差公式a2-b2=(a+b)(a-b)的熟练运用,此题比较简单,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.若x是不为0的有理数,已知M=(x2+1)(x2-1),N=(x2+1)2,则M与N的大小关系是( )
| A. | M>N | B. | M<N | C. | M=N | D. | 无法确定 |
17.下列各组数中,相等的是( )
| A. | -(-2)2=22 | B. | |-3|与-(-3) | C. | $\frac{3^2}{4}$与$\frac{9}{16}$ | D. | (-4)2与-16 |
11. 如图,两个正方形边长分别为a、b,a+b=16,ab=48,图中阴影部分的面积为( )
如图,两个正方形边长分别为a、b,a+b=16,ab=48,图中阴影部分的面积为( )
 如图,两个正方形边长分别为a、b,a+b=16,ab=48,图中阴影部分的面积为( )
如图,两个正方形边长分别为a、b,a+b=16,ab=48,图中阴影部分的面积为( )| A. | 56 | B. | 72 | C. | 80 | D. | 104 |
 如图,边长为1的小正方形构成的网格中,半径为1的⊙O在格点上,则∠AED的正切值为$\frac{1}{2}$.
如图,边长为1的小正方形构成的网格中,半径为1的⊙O在格点上,则∠AED的正切值为$\frac{1}{2}$.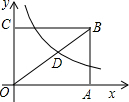 如图,已知矩形OABC面积为$\frac{100}{3}$,它的对角线OB与双曲线$y=\frac{k}{x}$相交于D且OB:OD=5:3,则k=( )
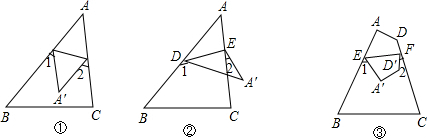
如图,已知矩形OABC面积为$\frac{100}{3}$,它的对角线OB与双曲线$y=\frac{k}{x}$相交于D且OB:OD=5:3,则k=( ) 如图所示,已知∠DAC=∠ACB,∠D=62°,求∠BCD的度数.
如图所示,已知∠DAC=∠ACB,∠D=62°,求∠BCD的度数.