题目内容
 如图,∠A=80°,∠ADB=60°,∠DBC=20°,AD=3,DC=2.则AB=( )
如图,∠A=80°,∠ADB=60°,∠DBC=20°,AD=3,DC=2.则AB=( )A、
| ||
B、
| ||
C、
| ||
| D、6 |
考点:相似三角形的判定与性质
专题:
分析:利用“两角法”推知△ABD∽△ADC,则根据该相似三角形的对应边成比例来求AB线段的长度即可.
解答: 解:如图,∵AD=3,DC=2,
解:如图,∵AD=3,DC=2,
∴AC=AD+DC=5.
∵∠A=80°,∠ADB=60°,
∴∠ABD=180°-∠A-∠ADB=40°,
又∵∠DBC=20°,
∴∠ABC=∠ABD+∠DBC=60°,
∴∠ABC=∠ADB.
又∠A=∠A,
∴△ABC∽△ADB,
∴
=
,即
=
,解得 AB=
故选:C.
 解:如图,∵AD=3,DC=2,
解:如图,∵AD=3,DC=2,∴AC=AD+DC=5.
∵∠A=80°,∠ADB=60°,
∴∠ABD=180°-∠A-∠ADB=40°,
又∵∠DBC=20°,
∴∠ABC=∠ABD+∠DBC=60°,
∴∠ABC=∠ADB.
又∠A=∠A,
∴△ABC∽△ADB,
∴
| AB |
| AD |
| AC |
| AB |
| AB |
| 3 |
| 5 |
| AB |
| 15 |
故选:C.
点评:本题考查了相似三角形的判定与性质.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件.

练习册系列答案
相关题目
借助一副三角尺,你能画出的角的度数是( )
| A、65° | B、15° |
| C、85° | D、95° |
下列几何体中:正方体,长方体,圆柱,六棱柱,圆锥,球,截面的形状可以为长方形的个数为( )
| A、3个 | B、4 | C、5个 | D、6个 |
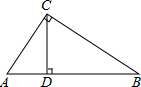 在Rt△ABC中,∠ACB=90°,CD⊥AB,
在Rt△ABC中,∠ACB=90°,CD⊥AB,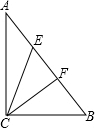 已知E、F是Rt△ABC斜边AB的三等分点,AE=EF=FB,且CE=4,CF=3,求斜边AB的长.
已知E、F是Rt△ABC斜边AB的三等分点,AE=EF=FB,且CE=4,CF=3,求斜边AB的长.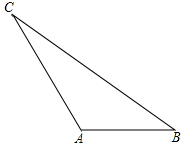 如图所示,在△ABC中,AB=1,AC=
如图所示,在△ABC中,AB=1,AC=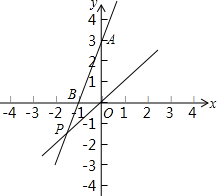 如图,已知y=3x+3与x轴交于点B,与y轴交于点A,与函数y=x的图象交于点P.
如图,已知y=3x+3与x轴交于点B,与y轴交于点A,与函数y=x的图象交于点P. 如图是由4个边长为1的正方形组成的图形,请求出∠ABC的度数.
如图是由4个边长为1的正方形组成的图形,请求出∠ABC的度数.