题目内容
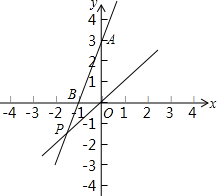 如图,已知y=3x+3与x轴交于点B,与y轴交于点A,与函数y=x的图象交于点P.
如图,已知y=3x+3与x轴交于点B,与y轴交于点A,与函数y=x的图象交于点P.(1)在该坐标系中画出函数y=
| 1 |
| 3 |
| 1 |
| 3 |
(2)设直线y=
| 1 |
| 3 |
(3)连接AC,则△APC的面积为
考点:两条直线相交或平行问题
专题:计算题
分析:(1)先用描点法画出函数y=
x-1的图象,再根据两直线相交的问题,通过解方程组
得到P点坐标为(-
,-
),然后根据一次函数图象上点的坐标特征判断点P在函数y=
x-1的图象上;
(2)利用点A和C的坐标特征可得点A和点C关于直线y=x对称,根据对称的性质可得直线y=x垂直平分AC,于是可得到PO平分∠APC;
(3)先确定B点坐标,然后根据三角形面积公式和△APC的面积=S△ABC+S△PBC进行计算.
| 1 |
| 3 |
|
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
(2)利用点A和C的坐标特征可得点A和点C关于直线y=x对称,根据对称的性质可得直线y=x垂直平分AC,于是可得到PO平分∠APC;
(3)先确定B点坐标,然后根据三角形面积公式和△APC的面积=S△ABC+S△PBC进行计算.
解答:(1)解:如图,
解方程组
得
,
则P点坐标为(-
,-
),
当x=-
时,y=
x-1=
×(-
)-1=-
,
所以点P在函数y=
x-1的图象上;
(2)证明:∵点A(0,3)和点C(3,0)关于直线y=x对称,
∴直线y=x垂直平分AC,
∴PO平分∠APC;
(3)解:B(-1,0),A(0,3),
△APC的面积=S△ABC+S△PBC
=
×(3+1)×3+
×(3+1)×
=9.
故答案为9.

解方程组
|
|
则P点坐标为(-
| 3 |
| 2 |
| 3 |
| 2 |
当x=-
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
所以点P在函数y=
| 1 |
| 3 |
(2)证明:∵点A(0,3)和点C(3,0)关于直线y=x对称,
∴直线y=x垂直平分AC,
∴PO平分∠APC;
(3)解:B(-1,0),A(0,3),
△APC的面积=S△ABC+S△PBC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=9.
故答案为9.
点评:本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
相关题目
2011年6月,全国参加高等院校统一招生考试的学生约10 200 000人,其中10 200 000用科学记数法表示应为( )
| A、10.2×106 |
| B、1.02×107 |
| C、0.102×108 |
| D、1.02×108 |
 如图,∠A=80°,∠ADB=60°,∠DBC=20°,AD=3,DC=2.则AB=( )
如图,∠A=80°,∠ADB=60°,∠DBC=20°,AD=3,DC=2.则AB=( )A、
| ||
B、
| ||
C、
| ||
| D、6 |
一次知识竞赛共有20道选择题,规定答对一道得5分,不做或错一题扣1分,结果某学生得分为88分,则他做对题数为( )
| A、16 | B、17 | C、18 | D、19 |
下列图形中,必是相似形的是( )
| A、都有一个角是40°的两个等腰三角形 |
| B、都有一个角为50°的两个等腰梯形 |
| C、都有一个角是30°的两个菱形 |
| D、邻边之比为2:3的两个平行四边形 |
下列说法中正确的是( )
| A、若|a|=|b|,则a=b |
| B、若ac=bc,则a=b |
| C、若线段AC=BC,则点C是线段AB的中点 |
| D、过n边形的一个顶点有(n-3)条对角线 |
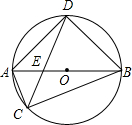 如图,△ABC内接于O⊙,AB为⊙O直径,CD平分∠ACB交⊙O于D,CD与AB交于点E,连接AD、BD.
如图,△ABC内接于O⊙,AB为⊙O直径,CD平分∠ACB交⊙O于D,CD与AB交于点E,连接AD、BD. 如图,∠B与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C进行同样的讨论.
如图,∠B与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C进行同样的讨论. 如图,圆O是三角形ABC的内切圆,求证:AB+CF=AC+BF.
如图,圆O是三角形ABC的内切圆,求证:AB+CF=AC+BF.