题目内容
如图是由4个边长为1的正方形组成的图形，请求出∠ABC的度数．考点：相似三角形的判定与性质
专题：
分析：由题意可求得AB、BC、DB，可证明△ABD∽△BCD，可得到∠BAD=∠CBD，再根据外角的性质可求得∠ABC．
解答：
解：由题意得AB=
BC=
；BD=
，
=
，
=
，
=
，
∴
=
=
，
∴△ABD∽△BCD，
∴∠BAD=∠CBD，
∴∠1=∠BAD+∠ABD=∠ABD+∠CBD=45°，
即∠ABC=45°．
解：由题意得AB=| 10； |
| 5 |
| 2 |
| AB |
| BC |
| 2 |
| AD |
| BD |
| 2 |
| BD |
| DC |
| 2 |
∴
| AB |
| BC |
| AD |
| BD |
| BD |
| DC |
∴△ABD∽△BCD，
∴∠BAD=∠CBD，
∴∠1=∠BAD+∠ABD=∠ABD+∠CBD=45°，
即∠ABC=45°．
点评：本题主要考查相似三角形的判定和性质，掌握相似三角形的对应边成比例、对应角相等是解题的关键．
练习册系列答案
相关题目
如图，∠A=80°，∠ADB=60°，∠DBC=20°，AD=3，DC=2．则AB=（ ）A、
| ||
B、
| ||
C、
| ||
| D、6 |
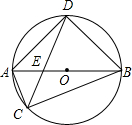如图，△ABC内接于O⊙，AB为⊙O直径，CD平分∠ACB交⊙O于D，CD与AB交于点E，连接AD、BD．
如图，∠B与哪个角是内错角，与哪个角是同旁内角？它们分别是哪两条直线被哪一条直线所截形成的？对∠C进行同样的讨论．
如图，一艘渔船正由西向东追赶鱼群，在A处测得小岛C在船的北偏东60°方向，距离A处80千米，此时渔船接到通知，以小岛C为中心周围30海里以内为我军导弹部队军事演习的着弹危险区，问这艘渔船继续向前追赶鱼群，是否有进入区域的可能？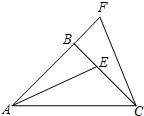
如图，△ABC中，AB=BC，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF
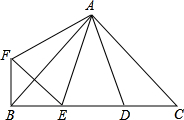如图，∠BAC=∠DAF=90°，AB=AC，AD=AF，点D、E为BC边上的两点，且∠DAE=45°，连接EF、BF、则下列结论：
如图，圆O是三角形ABC的内切圆，求证：AB+CF=AC+BF．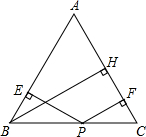
如图，已知等边三角形ABC中，P为底边BC上任意一点，PE⊥AB于E，PF⊥AC于F，BH⊥AC于H，求证：PE+PF=BH．