题目内容
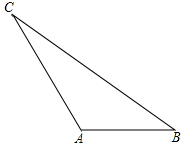 如图所示,在△ABC中,AB=1,AC=
如图所示,在△ABC中,AB=1,AC=| 2 |
| ||
| 4 |
考点:解直角三角形
专题:
分析:过点A作AE⊥BC,垂足为E,然后在Rt△ABE中,由AB=1,sinB=
,可求AE的值,然后由勾股定理得EB的值,然后在Rt△ACE中,根据勾股定理可得CE的值,然后将CE与BE相加即可.
| ||
| 4 |
解答:解:过点A作AE⊥BC,垂足为E,
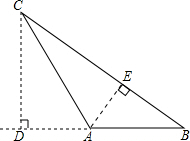
Rt△ABE中,
∵sinB=
=
,AB=1,
∴AE=
,
Rt△ABE中,
由勾股定理得:EB=
=
,
在Rt△ACE中,
∵AC=
,
由勾股定理得:CE=
=
,
∴BC=BE+CE=
.

Rt△ABE中,
∵sinB=
| AE |
| AB |
| ||
| 4 |
∴AE=
| ||
| 4 |
Rt△ABE中,
由勾股定理得:EB=
| AB2-AE2 |
| ||
| 4 |
在Rt△ACE中,
∵AC=
| 2 |
由勾股定理得:CE=
| AC2-AE2 |
| ||
| 4 |
∴BC=BE+CE=
| ||||
| 4 |
点评:此题考查了解直角三角形,解题的关键是:作辅助线将原三角形分成两个直角三角形,然后解直角三角形即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法错误的是( )
| A、1的平方根是±1 | ||
| B、只有非负数才有平方根和算术平方根 | ||
C、2的平方根是
| ||
D、±3是
|
 如图,∠A=80°,∠ADB=60°,∠DBC=20°,AD=3,DC=2.则AB=( )
如图,∠A=80°,∠ADB=60°,∠DBC=20°,AD=3,DC=2.则AB=( )A、
| ||
B、
| ||
C、
| ||
| D、6 |
下列图形中,必是相似形的是( )
| A、都有一个角是40°的两个等腰三角形 |
| B、都有一个角为50°的两个等腰梯形 |
| C、都有一个角是30°的两个菱形 |
| D、邻边之比为2:3的两个平行四边形 |
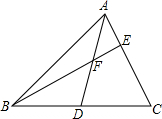 如图,AD是△ABC的中线,点E在AC上,BE交AD于点F.某数学兴趣小组在研究这个图形时得到如下结论:
如图,AD是△ABC的中线,点E在AC上,BE交AD于点F.某数学兴趣小组在研究这个图形时得到如下结论: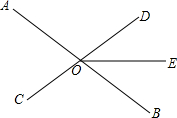 如图,直线AB、CD相交于点O,射线OE平分∠BOD.
如图,直线AB、CD相交于点O,射线OE平分∠BOD. 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3. 如图,一艘渔船正由西向东追赶鱼群,在A处测得小岛C在船的北偏东60°方向,距离A处80千米,此时渔船接到通知,以小岛C为中心周围30海里以内为我军导弹部队军事演习的着弹危险区,问这艘渔船继续向前追赶鱼群,是否有进入区域的可能?
如图,一艘渔船正由西向东追赶鱼群,在A处测得小岛C在船的北偏东60°方向,距离A处80千米,此时渔船接到通知,以小岛C为中心周围30海里以内为我军导弹部队军事演习的着弹危险区,问这艘渔船继续向前追赶鱼群,是否有进入区域的可能?