题目内容
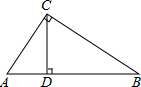 在Rt△ABC中,∠ACB=90°,CD⊥AB,
在Rt△ABC中,∠ACB=90°,CD⊥AB,(1)证明:△ADC∽△CDB;
(2)若CD=6,AB=13,求AD的长.
考点:相似三角形的判定与性质
专题:
分析:(1)由∠DCB+∠B=90°∠ACD+∠DCB=90°得出∠ACD=∠DCB,又因为∠CDB=∠CDA=90°即可证得结论.
(2)由△ADC∽△CDB得出CD2=AD•BD,从而求得AD的长.
(2)由△ADC∽△CDB得出CD2=AD•BD,从而求得AD的长.
解答:解:(1)∵CD⊥AB
∴∠CDB=∠CDA=90°,∠DCB+∠B=90°
又∵∠ACB=90°
∴∠ACD+∠DCB=90°
∴∠ACD=∠DCB
∴△ADC∽△CDB.
(2)由(1)可知,
=
即CD2=AD•BD
则62=AD•(13-AD)
解得:AD=4或6.
∴∠CDB=∠CDA=90°,∠DCB+∠B=90°
又∵∠ACB=90°
∴∠ACD+∠DCB=90°
∴∠ACD=∠DCB
∴△ADC∽△CDB.
(2)由(1)可知,
| AD |
| CD |
| CD |
| BD |
则62=AD•(13-AD)
解得:AD=4或6.
点评:本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定方法和性质定理是本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2011年6月,全国参加高等院校统一招生考试的学生约10 200 000人,其中10 200 000用科学记数法表示应为( )
| A、10.2×106 |
| B、1.02×107 |
| C、0.102×108 |
| D、1.02×108 |
 如图,∠A=80°,∠ADB=60°,∠DBC=20°,AD=3,DC=2.则AB=( )
如图,∠A=80°,∠ADB=60°,∠DBC=20°,AD=3,DC=2.则AB=( )A、
| ||
B、
| ||
C、
| ||
| D、6 |
 如图,在?ABCD中,E是BC边上的一点,且BE:EC=2:1,延长AE交DC延长线于点F,则AB:DF=
如图,在?ABCD中,E是BC边上的一点,且BE:EC=2:1,延长AE交DC延长线于点F,则AB:DF=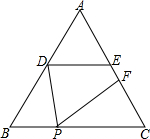 如图,在等边△ABC中,DE∥BC,分别交AB、AC于D、E,AD=3cm,BC=7cm,P为BC边上一动点(不与B、C重合),连结DP,过P点作PF交EC于F,使得∠DPF=∠B.
如图,在等边△ABC中,DE∥BC,分别交AB、AC于D、E,AD=3cm,BC=7cm,P为BC边上一动点(不与B、C重合),连结DP,过P点作PF交EC于F,使得∠DPF=∠B.