题目内容
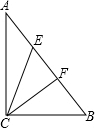 已知E、F是Rt△ABC斜边AB的三等分点,AE=EF=FB,且CE=4,CF=3,求斜边AB的长.
已知E、F是Rt△ABC斜边AB的三等分点,AE=EF=FB,且CE=4,CF=3,求斜边AB的长.考点:勾股定理
专题:
分析:延长CF到G,使FG=CF=3,连接EG并延长交AC与H,作DF⊥HG,由SAS定理得出△EFG≌△BFC,故EG=BC,∠G=∠BCF,同理可得△AHE≌△FDE,DF=AH,由平行线分线段成比例可知,HC=2DF,BC=3HE,设DF=AH=a,ED=EH=b,则HC=2a,EG=BC=3b,则DG=3b-b=2b,在Rt△CHE和Rt△FDG中根据勾股定理可知(2a)2+b2=42①,(2b)2+a2=32②,两式相加可得出EF的长,进而得出结论.
解答: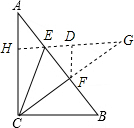 解:延长CF到G,使FG=CF=3,连接EG并延长交AC与H,作DF⊥HG,
解:延长CF到G,使FG=CF=3,连接EG并延长交AC与H,作DF⊥HG,
在△EFG与△BFC中,
∵
∴△EFG≌△BFC(SAS),
∴EG=BC,∠G=∠BCF,
∴GH∥BC,
∴GH⊥AC,
∴DF∥AC.
同理可得△AHE≌△FDE,
∴DF=AH,
由平行线分线段成比例可知,HC=2DF,BC=3HE,
设DF=AH=a,ED=EH=b,则HC=2a,EG=BC=3b,
∴DG=3b-b=2b,
在Rt△CHE和Rt△FDG中,(2a)2+b2=42①,(2b)2+a2=32②,
①+②得,a2+b2=5,即EF2=5,解得EF=
,
∴AB=3EF=3
.
 解:延长CF到G,使FG=CF=3,连接EG并延长交AC与H,作DF⊥HG,
解:延长CF到G,使FG=CF=3,连接EG并延长交AC与H,作DF⊥HG,在△EFG与△BFC中,
∵
|
∴△EFG≌△BFC(SAS),
∴EG=BC,∠G=∠BCF,
∴GH∥BC,
∴GH⊥AC,
∴DF∥AC.
同理可得△AHE≌△FDE,
∴DF=AH,
由平行线分线段成比例可知,HC=2DF,BC=3HE,
设DF=AH=a,ED=EH=b,则HC=2a,EG=BC=3b,
∴DG=3b-b=2b,
在Rt△CHE和Rt△FDG中,(2a)2+b2=42①,(2b)2+a2=32②,
①+②得,a2+b2=5,即EF2=5,解得EF=
| 5 |
∴AB=3EF=3
| 5 |
点评:本题考查的是勾股定理,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
2011年6月,全国参加高等院校统一招生考试的学生约10 200 000人,其中10 200 000用科学记数法表示应为( )
| A、10.2×106 |
| B、1.02×107 |
| C、0.102×108 |
| D、1.02×108 |
下列说法错误的是( )
| A、1的平方根是±1 | ||
| B、只有非负数才有平方根和算术平方根 | ||
C、2的平方根是
| ||
D、±3是
|
 如图,∠A=80°,∠ADB=60°,∠DBC=20°,AD=3,DC=2.则AB=( )
如图,∠A=80°,∠ADB=60°,∠DBC=20°,AD=3,DC=2.则AB=( )A、
| ||
B、
| ||
C、
| ||
| D、6 |
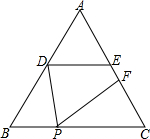 如图,在等边△ABC中,DE∥BC,分别交AB、AC于D、E,AD=3cm,BC=7cm,P为BC边上一动点(不与B、C重合),连结DP,过P点作PF交EC于F,使得∠DPF=∠B.
如图,在等边△ABC中,DE∥BC,分别交AB、AC于D、E,AD=3cm,BC=7cm,P为BC边上一动点(不与B、C重合),连结DP,过P点作PF交EC于F,使得∠DPF=∠B. 如图,在△ABC中,点D在边AB上,∠ACD=∠ABC,AD=1,AB=3.求AC的长.
如图,在△ABC中,点D在边AB上,∠ACD=∠ABC,AD=1,AB=3.求AC的长.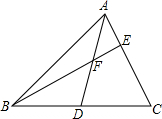 如图,AD是△ABC的中线,点E在AC上,BE交AD于点F.某数学兴趣小组在研究这个图形时得到如下结论:
如图,AD是△ABC的中线,点E在AC上,BE交AD于点F.某数学兴趣小组在研究这个图形时得到如下结论: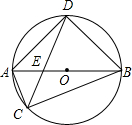 如图,△ABC内接于O⊙,AB为⊙O直径,CD平分∠ACB交⊙O于D,CD与AB交于点E,连接AD、BD.
如图,△ABC内接于O⊙,AB为⊙O直径,CD平分∠ACB交⊙O于D,CD与AB交于点E,连接AD、BD.