题目内容
4．写出并证明三角形中位线定理．分析 延长DE到点F使EF=DE，连接FC，DC，AF，证明四边形ADCF是平行四边形，得到四边形DBCF是平行四边形，证明结论．
解答 三角形中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半．
已知：如图，D，E分别是△ABC的边AB，AC的中点．
求证：DE∥BC，DE=$\frac{1}{2}$BC．
证明：如图，延长DE到点F使EF=DE，连接FC，DC，AF，
∵AE=EC，DE=EF，
∴四边形ADCF是平行四边形，
∴CF∥DA，CF=DA，
∴CF∥BD，CF=DB，
∴四边形DBCF是平行四边形，
∴DF∥BC．又DE=$\frac{1}{2}$DF，
∴DE∥BC，DE=$\frac{1}{2}$BC．
点评 本题考查的是三角形中位线定理的证明，掌握平行四边形的判定定理和性质定理是解题的关键．
练习册系列答案
相关题目
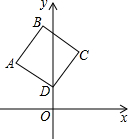如图，在正方形ABCD中，点D的坐标为（0，1），点A的坐标是（-2，2），则点B的坐标为（-1，4）．
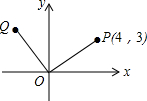如图所示，点P的坐标为（4，3），把点P绕坐标原点O逆时针旋转90°后得到点Q．
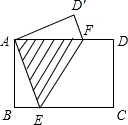如图，长方形纸片ABCD中，AB=3cm，BC=4cm，现将A，C重合，使纸片折叠压平，设折痕为EF，试确定重叠部分△AEF的面积．
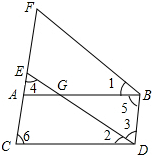如图，∠1=∠2，∠3=∠4，∠5=∠6．求证：ED∥FB．在下面的括号中填上推理依据．