题目内容
5.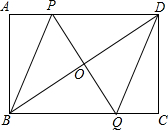 如图,矩形ABCD中,O为BD中点,PQ过点P分别交AD、BC于点P、Q,连接BP和DQ,求证:四边形PBQD是平行四边形.
如图,矩形ABCD中,O为BD中点,PQ过点P分别交AD、BC于点P、Q,连接BP和DQ,求证:四边形PBQD是平行四边形.
分析 依据矩形的性质和平行线的性质,通过全等三角形的判定定理判定△POD≌△QOB,所以OP=OQ,则四边形PBQD的对角线互相平分,故四边形PBQD为平行四边形.
解答 证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,
在△POD和△QOB中,
$\left\{\begin{array}{l}{∠PDO=∠QBO}\\{OB=OD}\\{∠POD=∠QOB}\end{array}\right.$,
∴△POD≌△QOB(ASA),
∴OP=OQ;
又∵O为BD的中点,
∴OB=OD,
∴四边形PBQD为平行四边形;
点评 本题考查了行四边形的判定、矩形的性质.凡是可以用平行四边形知识证明的问题,不要再回到用三角形全等证明,应直接运用平行四边形的性质和判定去解决问题.

练习册系列答案
相关题目
16.下列命题中的真命题是( )
| A. | 有一组对边平行的四边形是平行四边形 | |
| B. | 有一个角是直角的四边形是矩形 | |
| C. | 顺次连结矩形各中点所得的四边形是菱形 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
 如图,已知BC∥DE,∠ABC=120°,那么直线AB、DE的夹角是120°或60°.
如图,已知BC∥DE,∠ABC=120°,那么直线AB、DE的夹角是120°或60°.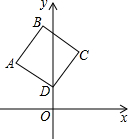 如图,在正方形ABCD中,点D的坐标为(0,1),点A的坐标是(-2,2),则点B的坐标为(-1,4).
如图,在正方形ABCD中,点D的坐标为(0,1),点A的坐标是(-2,2),则点B的坐标为(-1,4).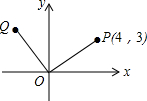 如图所示,点P的坐标为(4,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.
如图所示,点P的坐标为(4,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.