题目内容
3. 已知直线yOA=4x,yOB=x,分别反比例函数y=$\frac{k}{x}$于点A、B,若S△AOB=3,则k=4.
已知直线yOA=4x,yOB=x,分别反比例函数y=$\frac{k}{x}$于点A、B,若S△AOB=3,则k=4.
分析 设A的横坐标为m,B的横坐标为n,根据题意得出2m=n,过A、B分别作x的垂线,垂足分别为C、D,则CD=n-m,然后利用S△AOB=S梯形ABDC+S△ACO-S△BDO即可得到关于k的方程,解方程即可.
解答  解:∵直线yOA=4x,yOB=x,分别反比例函数y=$\frac{k}{x}$于点A、B,
解:∵直线yOA=4x,yOB=x,分别反比例函数y=$\frac{k}{x}$于点A、B,
∴设A的横坐标为m,B的横坐标为n
则4m=$\frac{k}{m}$,n=$\frac{k}{n}$,
解得2m=n,
过A、B分别作x的垂线,垂足分别为C、D,如图,
∵点A、B的横坐标分别为m、n,
∴CD=n-m,
∵S△AOB=S梯形ABDC+S△ACO-S△BDO=3,
∵S△ACO=S△BDO=$\frac{1}{2}$k
∴S梯形ABDC=3,即$\frac{1}{2}$($\frac{k}{m}$+$\frac{k}{n}$)(n-m)=3
∴k($\frac{1}{m}$+$\frac{1}{2m}$)(2m-m)=6,
∴$\frac{3}{2}$k=6,
∴k=4.
故答案为4.
点评 本题考查了一次函数和反比例函数的交点以及一次函数和反比例函数的性质:点在函数图象上,则点的横纵坐标满足其解析式.也考查了坐标与线段之间的关系以及不规则图形面积的计算方法.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
13.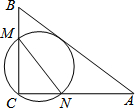 如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB,CA分别相交于点M,N,则线段MN长度的最小值是( )
如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB,CA分别相交于点M,N,则线段MN长度的最小值是( )
 如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB,CA分别相交于点M,N,则线段MN长度的最小值是( )
如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB,CA分别相交于点M,N,则线段MN长度的最小值是( )| A. | $\frac{16}{3}$ | B. | 5 | C. | $\frac{24}{5}$ | D. | $\frac{12}{5}$ |
18.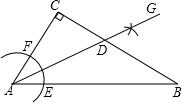 如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:
如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:
①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;
②分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径画弧,两弧相交于点G;
③作射线AG,交BC边于点D.
则∠ADC的度数为( )
 如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:
如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;
②分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径画弧,两弧相交于点G;
③作射线AG,交BC边于点D.
则∠ADC的度数为( )
| A. | 40° | B. | 55° | C. | 65° | D. | 75° |
15.为了看图钉落地后钉尖着地的概率有多大,小明做了大量重复试验,发现钉尖着地的次数是实验总次数的40%,下列说法错误的是( )
| A. | 钉尖着地的频率是0.4 | |
| B. | 随着试验次数的增加,钉尖着地的频率稳定在0.4附近 | |
| C. | 钉尖着地的概率约为0.4 | |
| D. | 前20次试验结束后,钉尖着地的次数一定是8次 |
12.下列计算中,正确的是( )
| A. | x2+x4=x6 | B. | 2x+3y=5xy | C. | (x3)2=x6 | D. | x6÷x3=x2 |
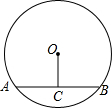 如图,⊙O的半径为5cm,圆心O到AB的距离为3cm,则弦AB长为8 cm.
如图,⊙O的半径为5cm,圆心O到AB的距离为3cm,则弦AB长为8 cm.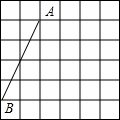 如图,点A、B为6×6的网格中的格点,每个小正方形的边长都为1,其中A点的坐标为(0,4).
如图,点A、B为6×6的网格中的格点,每个小正方形的边长都为1,其中A点的坐标为(0,4).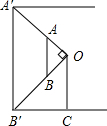 小明在数学课上学习了“相似三角形”这一节内容后,回家想用所学到的知识去测量他家小区路灯的高度,他带上了一个自制的直角三角板与皮尺对他家小区的路灯开始进行测量,通过观察可知路灯灯泡的高度与灯杆高度一致.首先,小明手拿自制直角三角板移动位置并观察,使三角板的顶点A与路灯最高点A′在一条线上,顶点B与路灯底端B′在一条线上,并记录下此时所在位置点C,再用皮尺测量出灯杆底端B′到C的距离为2m,小明知道自己的身高为1.6m(眼睛到头顶的距离可忽略不计),请你根据以上数据计算路灯高度A′B′.
小明在数学课上学习了“相似三角形”这一节内容后,回家想用所学到的知识去测量他家小区路灯的高度,他带上了一个自制的直角三角板与皮尺对他家小区的路灯开始进行测量,通过观察可知路灯灯泡的高度与灯杆高度一致.首先,小明手拿自制直角三角板移动位置并观察,使三角板的顶点A与路灯最高点A′在一条线上,顶点B与路灯底端B′在一条线上,并记录下此时所在位置点C,再用皮尺测量出灯杆底端B′到C的距离为2m,小明知道自己的身高为1.6m(眼睛到头顶的距离可忽略不计),请你根据以上数据计算路灯高度A′B′.