题目内容
13.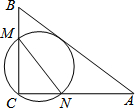 如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB,CA分别相交于点M,N,则线段MN长度的最小值是( )
如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB,CA分别相交于点M,N,则线段MN长度的最小值是( )| A. | $\frac{16}{3}$ | B. | 5 | C. | $\frac{24}{5}$ | D. | $\frac{12}{5}$ |
分析 设MN的中点为P,⊙P与AB的切点为D,连接PD,连接CP,CD,则有PD⊥AB;由勾股定理的逆定理知,△ABC是直角三角形PC+PD=MN,由三角形的三边关系知,PC+PD>CD;只有当点P在CD上时,PC+PD=MN有最小值为CD的长,即当点P在直角三角形ABC的斜边AB的高CD上时,MN=CD有最小值,由直角三角形的面积公式知,此时CD=BC•AC÷AB,进而求出即可.
解答 解:如图,设MN的中点为P,⊙P与AB的切点为D,连接PD,连接CP,CD,则有PD⊥AB;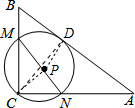
∵AB=10,AC=8,BC=6,
∴∠ACB=90°,PC+PD=MN,
∴PC+PD>CD,
∵当点P在直角三角形ABC的斜边AB的高CD上时,MN=CD有最小值,
∴CD=BC•AC÷AB=$\frac{24}{5}$.
故选C.
点评 此题主要考查了切线的性质,勾股定理的逆定理,三角形的三边关系,直角三角形的面积公式求解,得出CD=BC•AC÷AB是解题关键.

练习册系列答案
相关题目
1.把(-2)2014+(-2)2015分解因式的结果是( )
| A. | 22015 | B. | -22015 | C. | -22014 | D. | 22014 |
2.某商品每件的标价是440元,按标价的八折销售时,仍可获利10%,则这种商品每件的进价为( )
| A. | 240元 | B. | 280元 | C. | 320元 | D. | 360元 |
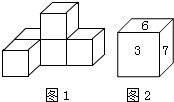 (1)画出下图1中几何体的三视图.
(1)画出下图1中几何体的三视图.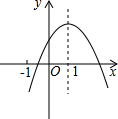 二次函数y=ax2+bx+c的图象如图所示,则在下列各不等式中成立的个数是( )
二次函数y=ax2+bx+c的图象如图所示,则在下列各不等式中成立的个数是( ) 已知直线yOA=4x,yOB=x,分别反比例函数y=$\frac{k}{x}$于点A、B,若S△AOB=3,则k=4.
已知直线yOA=4x,yOB=x,分别反比例函数y=$\frac{k}{x}$于点A、B,若S△AOB=3,则k=4.