题目内容
14．
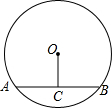如图，⊙O的半径为5cm，圆心O到AB的距离为3cm，则弦AB长为8 cm．
分析 连接OA，由OC垂直于弦AB，利用垂径定理得到C为AB的中点，在直角三角形AOC中，由OA与OC的长，利用勾股定理求出AC的长，即可得出AB的长．
解答 
解：连接OA，
∵OC⊥AB，
∴C为AB的中点，即AC=BC，
在Rt△AOC中，OA=5cm，OC=3cm，
根据勾股定理得：AC=$\sqrt{{OA}^{2}-{OC}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4cm，
∴AB=2AC=8cm．
故答案为：8．
点评 本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
2．某商品每件的标价是440元，按标价的八折销售时，仍可获利10%，则这种商品每件的进价为（ ）
| A． | 240元 | B． | 280元 | C． | 320元 | D． | 360元 |
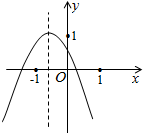如图所示的二次函数y=ax2+bx+c（a≠0）的图象中，胡娇同学观察得出了下面四条信息：（1）（a≠0）b2-4ac＞0；（2）c＞1；（3）2a-b＜0；（4）a+b+c＜0．你认为其中错误的信息有（ ）
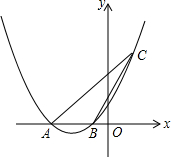如图，二次函数y=$\frac{1}{4}$x2+（$\frac{m}{4}$+1）x+m（其中m＜4）的图象与x轴相交于A、B两点，且点A在点B的左侧．
已知直线yOA=4x，yOB=x，分别反比例函数y=$\frac{k}{x}$于点A、B，若S△AOB=3，则k=4．