题目内容
18.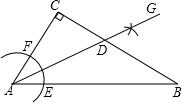 如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:
如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;
②分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径画弧,两弧相交于点G;
③作射线AG,交BC边于点D.
则∠ADC的度数为( )
| A. | 40° | B. | 55° | C. | 65° | D. | 75° |
分析 根据角平分线的作法可得AG是∠CAB的角平分线,然后再根据角平分线的性质可得∠CAD=$\frac{1}{2}$∠CAB=25°,然后再根据直角三角形的性质可得∠CDA=90°-25°=65°.
解答 解:根据作图方法可得AG是∠CAB的角平分线,
∵∠CAB=50°,
∴∠CAD=$\frac{1}{2}$∠CAB=25°,
∵∠C=90°,
∴∠CDA=90°-25°=65°,
故选:C.
点评 此题主要考查了基本作图,关键是掌握角平分线的作法,以及直角三角形的性质.关键是掌握直角三角形两锐角互余.

练习册系列答案
相关题目
9.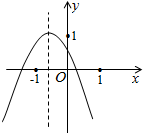 如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,胡娇同学观察得出了下面四条信息:(1)(a≠0)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的信息有( )
如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,胡娇同学观察得出了下面四条信息:(1)(a≠0)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的信息有( )
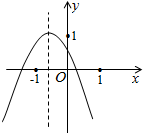 如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,胡娇同学观察得出了下面四条信息:(1)(a≠0)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的信息有( )
如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,胡娇同学观察得出了下面四条信息:(1)(a≠0)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的信息有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
8.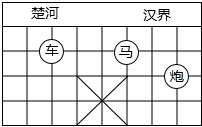 如图,已知棋子“车”的坐标为(-2,-1),棋子“马”的坐标为(1,-1),则棋子“炮”的坐标为( )
如图,已知棋子“车”的坐标为(-2,-1),棋子“马”的坐标为(1,-1),则棋子“炮”的坐标为( )
 如图,已知棋子“车”的坐标为(-2,-1),棋子“马”的坐标为(1,-1),则棋子“炮”的坐标为( )
如图,已知棋子“车”的坐标为(-2,-1),棋子“马”的坐标为(1,-1),则棋子“炮”的坐标为( )| A. | (3,2) | B. | (-3,2) | C. | (3,-2) | D. | (-3,-2) |
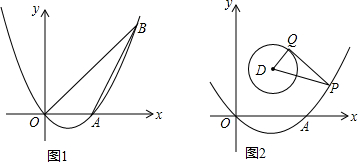
 如图,矩形ABCD中,AD=2AB
如图,矩形ABCD中,AD=2AB 已知直线yOA=4x,yOB=x,分别反比例函数y=$\frac{k}{x}$于点A、B,若S△AOB=3,则k=4.
已知直线yOA=4x,yOB=x,分别反比例函数y=$\frac{k}{x}$于点A、B,若S△AOB=3,则k=4.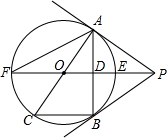 如图,PB为⊙O的切线,B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
如图,PB为⊙O的切线,B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.