题目内容
6. 如图,在△ABC中,AD平分∠BAC,AB+BD=AC,试讨论:∠B与∠C有什么样的等量关系?
如图,在△ABC中,AD平分∠BAC,AB+BD=AC,试讨论:∠B与∠C有什么样的等量关系?
分析 在AC上取一点E,使AE=AB,连接DE,则有EC=BD,证△ABD≌△AED,可以得出∠B=∠AED,BD=DE,则有DE=EC,∠EDC=∠C,∠AED=2∠C,得出结论.
解答  解:在AC上取一点E,使AE=AB,连接DE.
解:在AC上取一点E,使AE=AB,连接DE.
∵AB+BD=AC,
∴BD=AC-AB,
即BD=CE.
∵AD平分∠BAC,
∴∠BAD=∠EAD,
在△ABD和△AED中,
$\left\{\begin{array}{l}{AB=AE}\\{∠BAD=∠EAD}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△AED,
∴BD=DE,∠B=∠AED,
∴DE=EC,
∴∠C=∠EDC,
∵∠AED=∠C+∠EDC=2∠C,
∴∠B=2∠C.
点评 本题考查了截取法作辅助线的方法的运用,等腰三角形的性质,全等三角形的判定及性质,三角形的外角与内角的关系.

练习册系列答案
相关题目
15.抛物线y=ax2+bx+c(a<0)和直线y=mx+n(m≠0)相交于两点P(0,2)、Q(3,5),则不等式mx+n>ax2+bx+c的解集是( )
| A. | x<0 | B. | x>3 | C. | 0<x<3 | D. | x<0或x>3 |

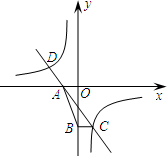 如图,直线y=kx+k(k≠0)与双曲线y=$\frac{n}{x}$(n<0)交于C、D两点,与x轴交于点A.
如图,直线y=kx+k(k≠0)与双曲线y=$\frac{n}{x}$(n<0)交于C、D两点,与x轴交于点A.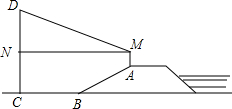 如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:$\sqrt{3}$,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30$\sqrt{3}$m.
如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:$\sqrt{3}$,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30$\sqrt{3}$m. 如图,AB=AE,BC=ED,AF⊥CD,∠B=∠E.F是CD的中点吗?为什么?
如图,AB=AE,BC=ED,AF⊥CD,∠B=∠E.F是CD的中点吗?为什么?