题目内容
8. 解答题
解答题如图所示,已知线段AB=12,C是线段AB上一点且线段AC=2,点D是线段CB的中点,点E是线段AD的中点,求线段CE的长度.
解:因为AB=12,AC=2,
所以CB=AB-AC=10.
因为点D是线段CB的中点,
所以CD=$\frac{1}{2}$CB=5.
所以AD=AC+CD=7.
又因为点E是线段AD的中点,
所以AE=$\frac{1}{2}$AD=$\frac{7}{2}$.
所以CE=AE-AC=$\frac{3}{2}$.
分析 根据线段的和差,可得CB,根据线段中点的性质,可得 CD的长,根据线段和差,可得AD的长,根据线段中点的性质,可得AE的长,再根据线段的和差,可得答案.
解答 解:因为AB=12,AC=2,
所以CB=AB-AC=10.
因为点D是线段CB的中点,
所以CD=$\frac{1}{2}$CB=5.
所以AD=AC+CD=7.
又因为点E是线段AD的中点,
所以AE=$\frac{1}{2}$AD=$\frac{7}{2}$.
所以CE=AE-AC=$\frac{3}{2}$,
故答案为:AC,10;CB,5;CD,7;AD,$\frac{7}{2}$;AC,$\frac{3}{2}$.
点评 本题考查了两点间的距离,利用线段和差、线段中点的性质是解题关键.

练习册系列答案
相关题目
16.16平方根是( )
| A. | 4 | B. | -4 | C. | ±4 | D. | ±8 |
17.下列运算正确的是( )
| A. | $\sqrt{1\frac{4}{9}}$=1+$\frac{2}{3}$ | B. | (-2x2)3=-6x6 | C. | ($\frac{1}{2}$)-2=4 | D. | (x-1)2=x2-12 |
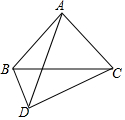 四边形ABCD中,∠BAC=∠BDC=90°,AB=AC,BD=2,DC=4,则AD=3$\sqrt{2}$.
四边形ABCD中,∠BAC=∠BDC=90°,AB=AC,BD=2,DC=4,则AD=3$\sqrt{2}$. 平行四边形是中心对称图形.如图,?ABCD以点O为旋转中心,按顺时针方向旋转180度后,与原来的图形能互相重合.
平行四边形是中心对称图形.如图,?ABCD以点O为旋转中心,按顺时针方向旋转180度后,与原来的图形能互相重合.