题目内容
19.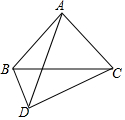 四边形ABCD中,∠BAC=∠BDC=90°,AB=AC,BD=2,DC=4,则AD=3$\sqrt{2}$.
四边形ABCD中,∠BAC=∠BDC=90°,AB=AC,BD=2,DC=4,则AD=3$\sqrt{2}$.
分析 过B作BF⊥AD于F,过C作CE⊥AD于E,得到∠AEC=∠AFB=90°,根据余角的性质得到∠BAF=∠ACE,推出△ABF≌△ACE,根据全等三角形的性质得到CE=AF,AE=BF,由∠BAC=∠BDC=90°,得到A,B,C,D四点共圆,根据圆周角定理得到∠ADB=∠ADC=45°,解直角三角形即可得到结论.
解答 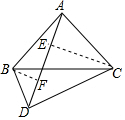 解:过B作BF⊥AD于F,过C作CE⊥AD于E,
解:过B作BF⊥AD于F,过C作CE⊥AD于E,
∴∠AEC=∠AFB=90°,
∵∠BAC=90°,
∴∠BAF+∠CAE=∠CAE+∠ACE=90°,
∴∠BAF=∠ACE,
在△ABF与△ACE中,$\left\{\begin{array}{l}{∠AFB=∠AEC}\\{∠ACE=∠BAF}\\{AB=AC}\end{array}\right.$,
∴△ABF≌△ACE,
∴CE=AF,AE=BF,
∵∠BAC=∠BDC=90°,
∴A,B,C,D四点共圆,
∴∠ADB=∠ADC=45°,
∴BF=DF=$\frac{\sqrt{2}}{2}$BD=$\sqrt{2}$,CE=DE=$\frac{\sqrt{2}}{2}$CD=2$\sqrt{2}$,
∴AD=AE+DE=BF+CE=3$\sqrt{2}$.
故答案为:3$\sqrt{2}$.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,四点共圆,正确的作出辅助线是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.下列说法正确的是( )
| A. | 有理数分为正数和负数 | B. | 有理数的相反数一定比0小 | ||
| C. | 绝对值相等的两个数不一定相等 | D. | 有理数的绝对值一定比0大 |
9.将350000用科学记数法表示为( )
| A. | 35×104 | B. | 3.5×105 | C. | 3.5×106 | D. | 0.35×106 |
 解答题
解答题