题目内容
5.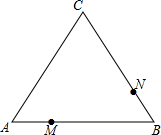 如图,在△ABC中,AB=30cm,BC=35cm,∠B=60°,有一动点M自A向B以1cm/s的速度运动,动点N自B向C以2cm/s的速度运动,若M,N同时分别从A,B出发.
如图,在△ABC中,AB=30cm,BC=35cm,∠B=60°,有一动点M自A向B以1cm/s的速度运动,动点N自B向C以2cm/s的速度运动,若M,N同时分别从A,B出发.(1)请你推算一下出发几秒后,△BMN为等边三角形?
(2)出发几秒后,△BMN为直角三角形?通过推算,你有什么结论?
分析 (1)因为∠B=60°,所以当△BMN为等边三角形时,BM=BN,据此来求点M、N的运动时间;
(2)需要分类讨论:∠BMN=90°和∠BNM=90°两种情况,利用直角三角形30°的性质解决问题.
解答 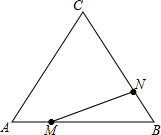 解:(1)当,△BMN为等边三角形时,BM=BN,
解:(1)当,△BMN为等边三角形时,BM=BN,
则设运动时间为t,依题意得:
30-t=2t,
解得t=10.
答:出发10秒后,△BMN为等边三角形;
(2)①当∠MNB=90°时,∵∠B=60°,
∴∠NMB=30°,
∴MB=2BN,
∴30-t=4t,
∴t=6,
②当∠NMB=90°时,∵∠B=60°,
∴∠MNB=30°,
∴BN=2BM,
∴2t=2(30-t),
∴t=15,
∴t=6或15秒时,△MNB是直角三角形.
点评 本题考查等边三角形的判定、直角三角形的判定、直角三角形30度角的性质,解题的关键是利用方程的思想解决问题,学会转化的思想,把问题转化为方程,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
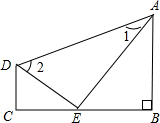 如图,AE平分∠BAD,DE平分∠ADC,AB⊥BC于B,∠1+∠2=90°,试判断DC与BC的位置关系,并加以说明.
如图,AE平分∠BAD,DE平分∠ADC,AB⊥BC于B,∠1+∠2=90°,试判断DC与BC的位置关系,并加以说明.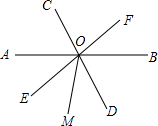 如图,直线AB,CD,EF相交于点O,∠BOD=64°,∠AOF=140°.
如图,直线AB,CD,EF相交于点O,∠BOD=64°,∠AOF=140°.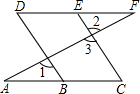 如图,若∠1=∠2,∠C=∠D,问∠A与∠F有什么关系?并说明理由.
如图,若∠1=∠2,∠C=∠D,问∠A与∠F有什么关系?并说明理由.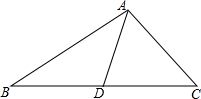 如图,AD是△ABC的中线,∠CAD=60°,AD=4,AB-AC=2,则BC的长为2$\sqrt{21}$.
如图,AD是△ABC的中线,∠CAD=60°,AD=4,AB-AC=2,则BC的长为2$\sqrt{21}$.