题目内容
13．方程组$\left\{\begin{array}{l}{4x-3y-3z=0}\\{x-3y+z=0}\end{array}\right.$（xyz≠0）中可以知道，x：z=4：3．分析 方程组两方程相减消去y，即可求出x与z的比值．
解答 解：$\left\{\begin{array}{l}{4x-3y-3z=0①}\\{x-3y+z=0②}\end{array}\right.$，
①-②得：3x-4z=0，
即x=$\frac{4}{3}$z，
则x：z=$\frac{4}{3}$z：z=4：3．
故答案为：4：3．
点评 此题考查了解三元一次方程组，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
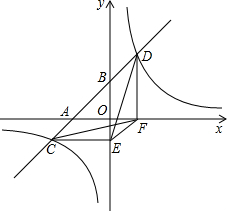如图，直线l与x轴、y轴交于A、B两点．与双曲线y=$\frac{k}{x}$和交于C、D两点，分别过C、D两点作y轴，x轴的垂线，垂足为E、F．连接CF、DE．则下列结论中：
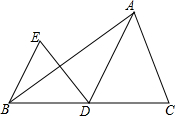如图，AD是△ABC中BC边上的中线，∠ADC为锐角，把△ADC沿直线AD折过来，点C落在点E的位置上．试猜想直线BE与直线DA的位置关系，并证明你的猜测．
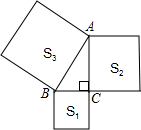如图，以Rt△ABC的三边为边向外作正方形，其面积分别为S1、S2、S3，且S1=10，S2=15，则AB的长为5．
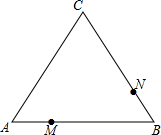如图，在△ABC中，AB=30cm，BC=35cm，∠B=60°，有一动点M自A向B以1cm/s的速度运动，动点N自B向C以2cm/s的速度运动，若M，N同时分别从A，B出发．
如图，AB∥CD，∠A=41°，∠C=32°，则∠AEC的大小为73度．