题目内容
9. 在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AD是∠BAC的平分线,若P、Q分别是AD和AC上的动点,则PC+PQ的最小值是2.4.
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AD是∠BAC的平分线,若P、Q分别是AD和AC上的动点,则PC+PQ的最小值是2.4.
分析 如图作CQ′⊥AB于Q′交AD于点P,作PQ⊥AC此时PC+PQ最短,利用面积法求出CQ′即可解决问题.
解答 解:如图,作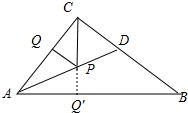 CQ′⊥AB于Q′交AD于点P,作PQ⊥AC此时PC+PQ最短.
CQ′⊥AB于Q′交AD于点P,作PQ⊥AC此时PC+PQ最短.
∵PQ⊥AC,PQ′⊥AB,AD平分∠CAB,
∴PQ=PQ′,
∴PQ+CP=PC+PQ′=CQ′
∴此时PC+PQ最短(垂线段最短).
在RT△ABC中,∵∠ACB=90°,AC=3,BC=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵$\frac{1}{2}$•AC•BC=$\frac{1}{2}$•AB•CQ′,
∴CQ′=$\frac{AC•CB}{AB}$=$\frac{12}{5}$=2.4.
∴PC+PQ的最小值为2.4.
故答案为2.4.
点评 本题考查轴对称-最短问题、角平分线性质、勾股定理等知识,解题的关键是找到点P、Q的位置,灵活应用垂线段最短解决问题,属于中考常考题型.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
19.如果∠1与∠2互为补角,∠1>∠2,那么∠2的余角等于( )
| A. | $\frac{1}{2}$(∠1+∠2) | B. | $\frac{1}{2}$∠1 | C. | $\frac{1}{2}$(∠1-∠2) | D. | ∠1-∠2 |
17.在实数0,π,$\frac{1}{3}$,$\sqrt{2}$,-$\sqrt{9}$中,无理数的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 按要求完成下列证明
按要求完成下列证明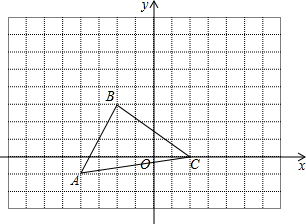 如图,三角形ABC中,任意移动P(x0,y0)经平移后对应点为P0(x0+5,y0+3).将三角形ABC作同样的平移后得到三角形A1B1C1.
如图,三角形ABC中,任意移动P(x0,y0)经平移后对应点为P0(x0+5,y0+3).将三角形ABC作同样的平移后得到三角形A1B1C1. 如图,在平面直角坐标系中,三角形ABC的三个顶点的坐标分别为A(-2,5)、B(-4,3)、C(-1,1),请作出三角形ABC向右平移5个单位后得到的三角形A1B1C1,并求出三角形ABC的面积.
如图,在平面直角坐标系中,三角形ABC的三个顶点的坐标分别为A(-2,5)、B(-4,3)、C(-1,1),请作出三角形ABC向右平移5个单位后得到的三角形A1B1C1,并求出三角形ABC的面积.