题目内容
17．在实数0，π，$\frac{1}{3}$，$\sqrt{2}$，-$\sqrt{9}$中，无理数的有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
解答 解：π，$\sqrt{2}$是无理数，
故选：B．
点评 此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．
练习册系列答案
阅读快车系列答案
相关题目
8．有下列各式（1）$\sqrt{{{（a+2b）}^2}}$=a+2b（2）$\sqrt{{x^2}-4}=\sqrt{x+2}•\sqrt{x-2}$（3）$\sqrt{\frac{3a}{b}}=\frac{1}{b}\sqrt{3ab}$，其中一定成立的有
（ ）
（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
5．下列几何体中，主视图是等腰三角形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
12．
轮船从B处以每小时25海里的速度沿南偏东30°方向匀速航行，在B处观测灯塔A位于南偏东75°方向上，轮船航行1小时到达C处，在C处观测灯塔A位于北偏东60°方向上，则C处于灯塔A的距离是（ ）海里．
轮船从B处以每小时25海里的速度沿南偏东30°方向匀速航行，在B处观测灯塔A位于南偏东75°方向上，轮船航行1小时到达C处，在C处观测灯塔A位于北偏东60°方向上，则C处于灯塔A的距离是（ ）海里．| A． | 25$\sqrt{3}$ | B． | 25$\sqrt{2}$ | C． | 25 | D． | 50 |
2．
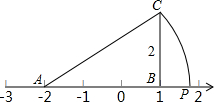如图，数轴上A表示数-2，过数轴上表示1的点B作BC⊥x轴，若BC=2，以A为圆心，AC为半径作圆弧交数轴于点P，那么数轴上点P所表示的数是（ ）
如图，数轴上A表示数-2，过数轴上表示1的点B作BC⊥x轴，若BC=2，以A为圆心，AC为半径作圆弧交数轴于点P，那么数轴上点P所表示的数是（ ）| A． | $\sqrt{13}$ | B． | $\sqrt{13}$-2 | C． | $\sqrt{13}$-3 | D． | 4-$\sqrt{13}$ |
在Rt△ABC中，∠ACB=90°，AC=3，BC=4，AD是∠BAC的平分线，若P、Q分别是AD和AC上的动点，则PC+PQ的最小值是2.4．
已知：如图，平行四边形ACBD中，对角线AC、BD相交于点O，延长CD至F，使DF=CD，连接BF交AD于点E．
7．下列各题去括号所得结果正确的是（ ）
| A． | x2-（x-y+2z）=x2-x+y+2z | B． | x-[-y+（-3x+1）]=x+y+3x-1 | ||
| C． | 3x-[5x-（x-1）]=3x-5x-x+1 | D． | （x-1）-（x2-2）=x-1-x2-2 |