题目内容
4. 按要求完成下列证明
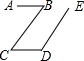
按要求完成下列证明如图,AB∥CD,CB∥DE,求证:∠B+∠D=180°.
证明:∵AB∥CD,
∴∠B=∠C(两直线平行,内错角相等).
∵CB∥DE,
∴∠C+∠D=180°(两直线平行,同旁内角互补).
∴∠B+∠D=180°.
分析 直接利用平行线的性质分别得出各角之间的关系,进而得出答案.
解答 证明:∵AB∥CD,
∴∠B=∠C (两直线平行,内错角相等),
∵CB∥DE,
∴∠C+∠D=180°(两直线平行,同旁内角互补),
∴∠B+∠D=180°.
故答案为:∠C,两直线平行,内错角相等;∠D;两直线平行,同旁内角互补.
点评 此题主要考查了平行线的性质,正确把握平行线的性质是解题关键.

练习册系列答案
相关题目
12. 轮船从B处以每小时25海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行1小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处于灯塔A的距离是( )海里.
轮船从B处以每小时25海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行1小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处于灯塔A的距离是( )海里.
 轮船从B处以每小时25海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行1小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处于灯塔A的距离是( )海里.
轮船从B处以每小时25海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行1小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处于灯塔A的距离是( )海里.| A. | 25$\sqrt{3}$ | B. | 25$\sqrt{2}$ | C. | 25 | D. | 50 |
16. 如图,在平行四边形ABCD中,下列结论错误的是( )
如图,在平行四边形ABCD中,下列结论错误的是( )
 如图,在平行四边形ABCD中,下列结论错误的是( )
如图,在平行四边形ABCD中,下列结论错误的是( )| A. | ∠ABD=∠BDC | B. | AC⊥BD | C. | AB=CD | D. | ∠BAD=∠BCD |
13. 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )
 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
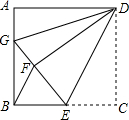 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,则BG=8.
如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,则BG=8. 在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AD是∠BAC的平分线,若P、Q分别是AD和AC上的动点,则PC+PQ的最小值是2.4.
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AD是∠BAC的平分线,若P、Q分别是AD和AC上的动点,则PC+PQ的最小值是2.4.