题目内容
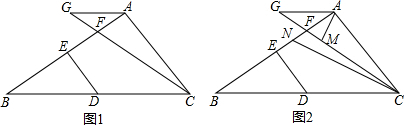
17. 如图,三个全等的直角三角形正好拼成一个直角△ABC,其中,∠A=90°,那么∠C的度数为30°.
如图,三个全等的直角三角形正好拼成一个直角△ABC,其中,∠A=90°,那么∠C的度数为30°.
分析 因为三个全等的直角三角形正好拼成一个直角△ABC,所以△BAE≌△BDE≌△CDE,由全等三角形的性质可得∠ABE=∠EBD=∠DCE,再由三角形内角和为180°,即可求出∠C的度数.
解答 解:
∵三个全等的直角三角形正好拼成一个直角△ABC,
∴△BAE≌△BDE≌△CDE,
∴∠ABE=∠EBD=∠DCE,
∵∠A=90°,
∴∠ABE+∠EBD+∠C=90°,
∴3∠C=90°,
∴∠C=30°,
故答案为:30°.
点评 本题考查了图形的剪拼和全等三角形的性质以及三角形内角和定理的运用,题目设计比较新颖,熟记全等三角形的各种性质是解题的关键.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
5.以下说法:
①两点确定一条直线;
②一条直线有且只有一条垂线;
③不相等的两个角一定不是对顶角;
④若|a|=-a,则a<0;
⑤若a,b互为相反数,则a,b的商必定等于-1.
其中正确的是①③.(请填序号)
①两点确定一条直线;
②一条直线有且只有一条垂线;
③不相等的两个角一定不是对顶角;
④若|a|=-a,则a<0;
⑤若a,b互为相反数,则a,b的商必定等于-1.
其中正确的是①③.(请填序号)
2.已知:4x=9y=6,则$\frac{1}{x}$+$\frac{1}{y}$等于( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
18.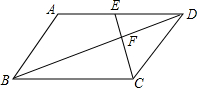 如图,在平行四边形ABCD中,E为AD的中点,△DEF的周长为1,则△BCF的周长为( )
如图,在平行四边形ABCD中,E为AD的中点,△DEF的周长为1,则△BCF的周长为( )
 如图,在平行四边形ABCD中,E为AD的中点,△DEF的周长为1,则△BCF的周长为( )
如图,在平行四边形ABCD中,E为AD的中点,△DEF的周长为1,则△BCF的周长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 根据如图所示的计算程序,若输出的值为5,则输入的值为10或-2.
根据如图所示的计算程序,若输出的值为5,则输入的值为10或-2.